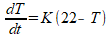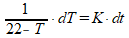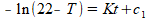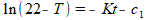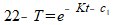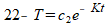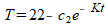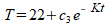WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Algemene oplossing differentiaalvergelijking

Hoi,

Ik zit hier met een oefententamen voor me van wiskunde, maar ik kom absoluut niet uit de opgave. Zou iemand hier mij de absolute oplossing van kunnen uitleggen?
^dT/_dT= K·(22-T)

Alvast heel hartelijk bedankt!
Lars
Student hbo - donderdag 22 juni 2017

Antwoord

Hallo Lars,

Allereerst: let op het juiste gebruik van hoofdletters en kleine letters. ^dT/_dT (zoals je noteert) is gewoon 1. Ik neem aan dat het hier gaat om temperatuur (aangeduid met hoofdletter T) en tijd (aangeduid met kleine letter t). In dat geval gaat het om de differentiaalvergelijking:

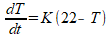
Deze kunnen we oplossen door middel van 'scheiden van variabelen', ofwel: alles met T naar links en alles met t naar rechts:

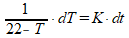
Dan kunnen we links en rechts primitiveren:

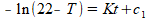
ofwel:

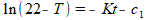
Volgens de definitie van de ln-functie geldt dan:

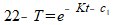
Anders geschreven:

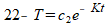
Isoleren van T levert dan:

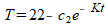
Omdat c₂ een nader te bepalen constante is, heeft het min-teken voor c₂ geen echte betekenis. We kunnen ook schrijven:

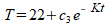
c₃ is dan het (temperatuur)verschil tussen T en 22 wanneer t=0. Het getal 22 is de waarde waartoe T nadert voor grote waarden van t.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 23 juni 2017