WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoek tussen twee rechten

Beste,

Kan u mij uitleggen hoe ik de hoek kan bepalen tussen de twee rechten met als voorschrift

a: 2x-y+3=0
b: -x+2y-8=0

Dit is een vraag uit mijn cursusdeel over het inproduct van vectoren (analytisch en meetkundig) dus ik denk dat het hiermee te maken heeft.

Alvast bedankt
Emile
2de graad ASO - zaterdag 10 juni 2017

Antwoord

Hallo Emile,

Het inproduct van twee richtingsvectoren a en b kan je berekenen met:

inproduct = x_ax_b + y_ay_b

maar ook met:

inproduct = |a|·|b|·cos($\alpha$)

waarbij $\alpha$ de ingesloten hoek is tussen de beide richtingsvectoren.

Wanneer je beide manieren van berekenen aan elkaar gelijk stelt en vervolgens cos($\alpha$) isoleert, dan krijg je:

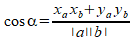
Met deze formule kan je dus de cosinus berekenen van de ingesloten hoek tussen twee richtingsvectoren, en daarmee de hoek zelf.

Richtingsvectoren van de gegeven lijnen zijn:
r_a=(1,2)
r_b=(2,1)

Laat hierop de formule los en je vindt de hoek tussen de richtingsvectoren.

Het is de gewoonte om als hoek tussen lijnen de kleinste hoek te nemen (dus: de scherpe hoek). Het kan zijn dat je een hoek vindt die groter is dan 90°, dus de stompe hoek tussen de lijnen. Trek dan jouw gevonden hoek van 180° af om de supplementaire hoek te vinden.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 10 juni 2017