WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Gooien met één dobbelsteen

Bij wiskunde kregen we de volgende opdracht: Hans en Peter hebben allebei een ‘gewone’ dobbelstenen met zes vlakken en op die vlakken res- pectievelijk 1, 2, 3, 4, 5 of 6 ogen, gooien deze, en wie het hoogste aantal ogen gooit wint. De ene keer wint Peter, de andere keer Hans. Als ze maar vaak genoeg spelen, dan zullen ze allebei bij benadering de helft van de keren winnen. Dat vindt Hans niet prettig.
Hans tekent bij het zijvlak met 2 ogen een oogje erbij. Hij speelt nu dus met 1, 3, 3, 4, 5, 6. Peter nog steeds met 1, 2, 3, 4, 5, 6. Zal Hans nu op den duur vaker winnen, of maakt het niet uit?
Peter heeft door dat Hans een extra oogje gezet heeft op het zijvlak van de 2 ogen. Daarom gaat hij ook op ́e ́en van de zijvlakken een oogje erbij zetten. Op welke zijde kan hij het beste een oogje erbij te tekenen om zo vaak mogelijk te winnen, die met 1, 2, 3, 4, 5 of 6? Waarom?
Ik kom hier echt niet uit, Hopelijk is er iemand die me kan helpen?
Jelmer
Leerling bovenbouw havo-vwo - dinsdag 23 mei 2017

Antwoord

Hallo Jelmer,

Hieronder heb ik een schema getekend met alle mogelijke uitkomsten, wanneer Hans en Peter met eerlijke dobbelstenen gooien. De vakjes met H geven aan dat Hans wint, een P geeft aan dat Peter wint. Een leeg vakje betekent gelijk spel:

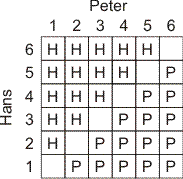
Elk vakje heeft dezelfde kans (1/36). Je ziet dat er evenveel H-tjes als P-tjes zijn, dus Hans en Peter hebben evenveel kans om te winnen.

De volgende figuur geeft de situatie weer wanneer Hans zijn '2 ogen' verandert in '3 ogen'. De veranderingen zijn in kleur weergegeven.

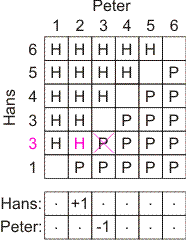
In het onderste schema heb ik aangegeven wat er per kolom is veranderd: er is één H-tje bijgekomen, er is één P-tje minder. De kans van Hans is dus 1/36 groter geworden, de kans van Peter is 1/36 kleiner geworden. De kansen op winst zijn dus veranderd!

Vraag b) kan je op dezelfde manier aanpakken. Hieronder staat nogmaals het schema waarbij Hans zijn '2 ogen' in '3 ogen' heeft veranderd.

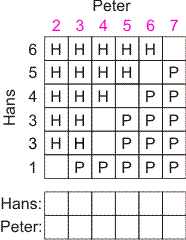
Neem nu eens aan dat Peter van zijn '1 oog' een '2 ogen' maakt (zie de gekleurde 2 boven de eerste kolom). Kijk wat er in de uitslagen in de eerste kolom verandert, en noteer je verandering in het onderste schema (in de kolommen 2 t/m 5 verandert natuurlijk niets).
Doe het zelfde voor de andere kolommen, en noteer per kolom steeds de verandering in het onderste schema. Dan blijkt vanzelf bij welke verandering de meeste P-tjes erbij komen en/of de meeste H-tjes eraf gaan. Dat is voor Peter dan de verstandigste keuze.

Veel succes!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 23 mei 2017