WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Een toepassing van de differentiaalrekening

Geachte mevrouw/meneer,

In mijn wiskundeboek staat de volgende opgave:

'Twee middelgrote steden A en B die aan dezelfde kant van een rivier liggen, willen een gemeenschappelijke waterkrachtcentrale aan de rivieroever bouwen. De rivieroever beschouwen we als een rechte lijn. De afstand tussen A en de rivieroever is 1 km, tussen B en de oever 4 km en de afstand tussen de steden is 8 km. Toon aan dat de kleinste, totale lengte van de leidingen van A en B tot de waterkrachtcentrale 4√5 km is.'

Ik ben begonnen met het uitzetten van de gegevens in een tekening. Echter kom ik daaruit niet verder. Ik zie geen enkel verband in de tekening behalve dat er een driehoek zichtbaar is tussen A en B en de rivieroever. Dat verklaart wel dat ik een wortel als antwoord kan krijgen door middel van de stelling van Pythagoras. Verder heb ik geen idee hoe ik verder kan komen.

Bedankt voor de moeite.

Met vriendelijke groet
Erwin
Student hbo - zondag 14 mei 2017

Antwoord

Ik heb maar even een tekening gemaakt.

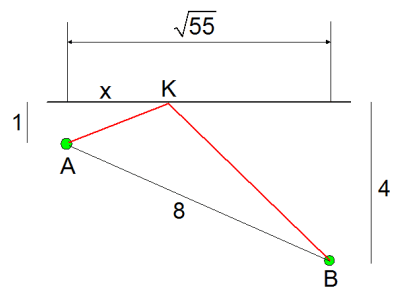
Het plan!

Druk $AK+BK$ uit in $x$. Bepaal de afgeleide. Stel de afgeleide op nul. Los de vergelijking op. Vul je oplossing in de uitdrukkking voor de lengte van $AK+BK$ in en je krijgt $4\sqrt{5}$ als antwoord.

Echt, het werkt...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 14 mei 2017