WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differentialen

Beste mevrouw/meneer,

In mijn wiskundeboek staat de volgende opgave: 'Bepaal de punten op de kromme x² - xy + y² = 27 waarin de raaklijn horizontaal respectievelijk verticaal loopt.'

Het eerste wat ik heb gedaan is de formule te differentiëren met behulp van differentialen (om zodoende de richtingscoëfficiënt van de raaklijnen te bepalen). Hieruit kwam de volgende formule:
^dy/_dx=-^2x-y/_x+2y

Nu ik de formule gedifferentieerd heb, komt het probleem dat ik te maken heb met twee variabelen. Ik weet dat als ik de teller 0 maak, de uitkomst van de breuk 0 en zodoende de verandering van de kromme 0 is. Hetzelfde geldt als ik de noemer 0 maak, de uitkomst van de breuk $\infty$ en zodoende de verandering van de kromme $\infty$ is.

Ik weet nu niet hoe ik de coördinaten kan berekenen van deze punten waar de raaklijnen oneindig en niet veranderen.

Alvast bedankt voor de moeite.

Met vriendelijke groet
Erwin
Student hbo - zaterdag 13 mei 2017

Antwoord

Ik kom uit op:

$
\eqalign{
& x^2 - xy + y^2 = 27 \cr
& 2x - y - xy' + 2yy' = 0 \cr
& - xy' + 2yy' = - 2x + y \cr
& y'( - x + 2y) = - 2x + y \cr
& y' = \frac{{ - 2x + y}}
{{ - x + 2y}} \cr
& y' = \frac{{2x - y}}
{{x - 2y}} \cr}
$

Dit geeft:
$y'=0$ voor $y=2x$
$y'=\infty$ voor $y=\frac{1}{2}x$

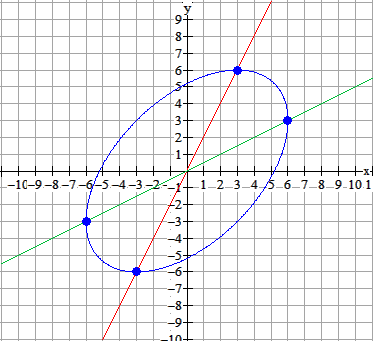
...en dan ben je er wel...

Berekenen kan zo:

$
\begin{array}{l}
\left\{ \begin{array}{l}
x^2 - xy + y^2 = 27 \\
y = 2x \\
\end{array} \right. \\
x^2 - x \cdot 2x + \left( {2x} \right)^2 = 27 \\
x^2 - 2x^2 + 4x^2 = 27 \\
3x^2 = 27 \\
x^2 = 9 \\
\left\{ \begin{array}{l}
x = - 3 \\
y = - 6 \\
\end{array} \right. \vee \left\{ \begin{array}{l}
x = 3 \\
y = 6 \\
\end{array} \right. \\
\end{array}
$

...evenzo...

$
\begin{array}{l}
\left\{ \begin{array}{l}
x^2 - xy + y^2 = 27 \\
x = 2y \\
\end{array} \right. \\
\left( {2y} \right)^2 - 2y \cdot y + y^2 = 27 \\
4y^2 - 2y^2 + y^2 = 27 \\
3y^2 = 27 \\
y^2 = 9 \\
\left\{ \begin{array}{l}
x = - 6 \\
y = - 3 \\
\end{array} \right. \vee \left\{ \begin{array}{l}
x = 6 \\
y = 3 \\
\end{array} \right. \\
\end{array}
$

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 13 mei 2017