WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Bol in een kegel

Hoi,

We hebben van de docent de volgende opdracht gekregen, maar we komen er niet echt uit:

Gevraagd de hoogte en de inhoud van de kleinste kegel, die men om een bol met straal r kan beschrijven.

We zijn zover dat we de doorsnede hebben getekend, we hebben wat dingen gesteld maar we schieten niet echt op. Iemand een idee hoe te beginnen aan deze som?

Met vriendelijke groet.
Didier
Leerling bovenbouw havo-vwo - donderdag 11 mei 2017

Antwoord

Hallo Didier,

Als het goed is, heb je deze dwarsdoorsnede:

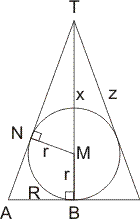
Hierin is:
R: straal grondvlak van de kegel (=AB)
r: straal van de bol
z: afstand tussen rand van het grondvlak en de top T
x: afstand tussen middelpunt M van de bol en de top T
Bedenk dan dat de driehoeken ABT en MNT gelijkvormig zijn (bedenk zelf waarom!). Dan geldt:

z/R = x/r

dus z = ^x/_r·R

volgens Pythagoras geldt ook:

(r+x)² + R² = z²

Wanneer we z uit de eerste formule in de tweede invullen, krijgen we:

(r+x)² + R² = (x/r)²·R²

Je kunt R² isoleren. De uitdrukking die je dan krijgt, kan je invullen in de formule voor de inhoud van een kegel:

I = ¹/₃$\pi$R²·h

met h=r+x

In deze formule is x de enige onbekende. Met behulp van de afgeleide kan je de waarde van x vinden waarvoor de inhoud van de kegel minimaal is, dan weet je natuurlijk ook R.

Kan je hiermee verder?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 11 mei 2017

Re: Bol in een kegel