WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Loodrechte lijnen

wij hebben een praktische opdracht dat gaat over de normalen de vraag luidt:

1a. Teken de lijn l: y=2a op ruitjespapier. Draai deze lijn 90 graden om de oorsprong en bepaal de richtingscoeffient (rico) van de gevonden lijn l’.
b. Teken door een willekeuring punt P op l een lijn l” die evenwijdig is aan lijn l’. Welke conclusie kun je trekken aangaande de rico’s van l enerzijds en l’ en l” anderzijds? Bewijs nu: elke lijn l’ die loodrecht staat op de lijn l: y =mx heeft rico…
Defenitie: een lijn ‘ die (in een gegeven punten) loodrecht staat op een gegeven lijn l heet een normaal van

Bij 1a en 1b is het tekenen wel gelukt, maar ik weet nu hoe ik moet bewijzen dat elke lijn l’ die loodrecht staat op de lijn l: y =mx heeft rico…
De Defenitie luidt: een lijn ‘ die (in een gegeven punten) loodrecht staat op een gegeven lijn l heet een normaal van l.

Ik hoop dat ik op deze manier de vraag duidelik heb gesteld!

Groetjes Amelia

Amelia
Leerling bovenbouw havo-vwo - dinsdag 11 maart 2003

Antwoord

Het klinkt allemaal heel ingewikkeld, maar is het niet zoiets:

Als l:y=ax, m:y=bx en l ^ m, dan a·b=-1

Voorbeeld
Teken de lijn l:y=2x, deze lijn gaat door de oorsprong. Als door de oorsprong een lijn tekent loodrecht op l, dan kan je de richtingscoëfficient wel bepalen. Die blijkt -¹/₂ te zijn. 2·-¹/₂=-1.

Dus voor dit voorbeeld klopt het! Misschien kan je het nu voor het algemene geval ook bewijzen. Misschien helpt volgende tekening....

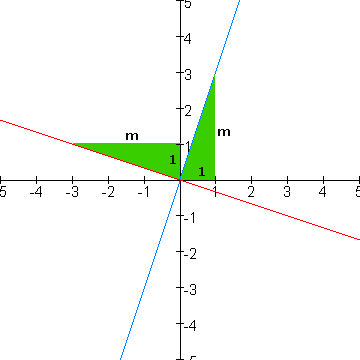
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 11 maart 2003