WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Speciale integrerende factor

Hoi,

Ik heb een vraag bij de integrerende factor van de volgende differentiaalvergelijking:

(3x²+y)dx + (x²y-x)dy=0

Deze differentiaalvergelijking is niet exact, maar kan door vermenigvuldiging met een integrerende factor omgevormd worden tot een totale differentiaalvergelijking.
Volgens het boek geldt er:
Als (My - Nx)/ N continu en enkel afhankelijk is van x, dan geldt er dat de integrerende factor gelijk is aan:
µ(x) = exp (∫(My - Nx)/ N dx)
Na wat rekenwerk is (Mx - Nx)/ N = -2/x.

Volgens de definitie zouden dus de volgende 2 kenmerken voldaan moeten zijn voordat we hierbij over kunnen gaan tot het berekenen van de integrerende factor:
- Enkel afhankelijk van x (OK!)
- Continu (NIET OK!)

Mijn vraag is nu:
Wat zal het effect zijn van het feit dat -2/x niet continu is in 0?
Kan je dan alsnog de integrerende factor bepalen?

In het handboek lijkt men dit wel te doen en bekomt men µ(x) = 1/x²

De algemene oplossing van de DV is dan 3x-y/x+(1/2)y²= c EN x≡0

Echter baart die x≡0 me wat zorgen...
Lene C
Student universiteit - maandag 13 maart 2017

Antwoord

De $\mu$ die je krijgt werkt alleen als $x\neq0$ en zal dus tot oplossingen leiden op twee aparte gebieden: 1) als $x $<$ 0$, en 2) als $x $>$ 0$.
Bij de formule die je krijgt moet je dat dan vermelden.
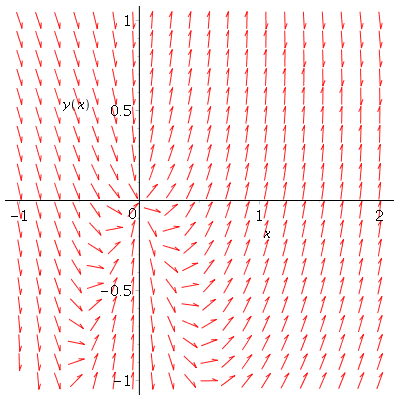
Als je de niveaukrommen van je oplossing tekent (of laat tekenen, door Maple of zo) zul je zien dan door de $y$-as geen oplossingen gaan.
Die $x=0$ bij je oplossing hoort daar eigenlijk niet; de oplossingen gelden alleen voor $x\neq0$.

Hieronder zie je een plaatje van het richtingsveld.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 13 maart 2017