|
|
|
\require{AMSmath}



Oplossen X in breuk
Hoe kom ik van:
$\$$ 1200 (1 + 0.11 ·(x/365)) – $\$$ 500 (1 + 0.11 ·((x-45)/365)) – $\$$ 300 (1 + 0.11 ·((x-100)/365))= $\$$ 436.92
Naar:
$\$$ 1200 + $\$$ 0.36164 x – $\$$ 500 – $\$$ 0.15068 x + $\$$ 6.78 – $\$$ 300 – $\$$ 0.09041 x + $\$$ 9.04 = $\$$ 436.92
$\$$ 415.82 + $\$$ 0.12055 x = $\$$ 436.92
--$>$ x = 175.031 = 175 days
Dit is het antwoord op de volgende vraag:
A debt of $\$$ 1200 is to be paid off by payments of $\$$ 500 in 45 days, $\$$ 300 in 100 days, and a final payment of $\$$ 436.92. The annual interest rate is 11 % and the Merchant’s Rule was used to calculate the final payment.
In how many days should the final payment be made using exact time to calculate exact simple interest?
Paula
Leerling bovenbouw havo-vwo - zondag 22 januari 2017
Antwoord
Hallo Paula,
Zorgvuldig haakjes wegwerken: netjes schrijven, en vooral in kleine stappen zodat je geen vergissingen maakt met min-tekens en zo:
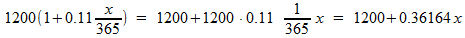
zo ook:
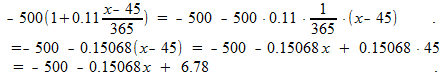
en:
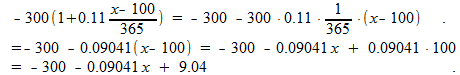
Dan deze drie resultaten 'bij elkaar vegen':
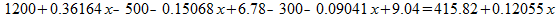
Je houdt een eenvoudige lineaire vergelijking over die je met de balansmethode kunt oplossen:
415.82 + 0.12055x = 436.92
x = 21.1/0.12055  175.031 175.031

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 22 januari 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








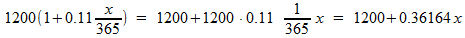
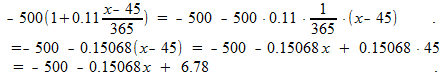
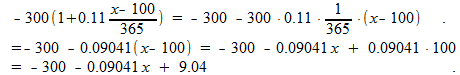
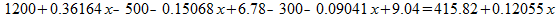
 175.031
175.031

