WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Absoluutstrepen binnen absoluutstrepen

De formule is : $y = 4-|3-|2x-6||$

Hiervan is gevraagd de grafiek te tekenen. Ik ben er zelf achtergekomen dat de grafiek 'omklapt' bij de x-waarden : 3 en 4,5. Nadat ik dit had uitgekregen heb ik de formule ingevoerd op de grafische rekenmachine en hem geplot. Echter hier komt een derde "omklapwaarde" uit namelijk de x-waarde: 1,5.

Nu is de vraag natuurlijk waarom ik deze waarde niet heb kunnen vinden. En of ik ergens op moet letten bij absoluutstrepen binnen absoluutstrepen.

Alvast bedankt!
De mam
Leerling bovenbouw havo-vwo - maandag 11 juli 2016

Antwoord

Gegeven is de functie: $f(x)=4-|3-|2x-6||$. Je kunt dan twee gevallen onderscheiden:

I. Als $2x-6\ge0$ dan $f(x)=4-|9-2x|$ voor $x\ge3$
II. Als $2x-6\lt0$ dan $f(x)=4-|-3+2x|$ voor $x\lt3$

Bij A. kan je dan weer twee gevallen onderscheiden:

i. Als $9-2x\ge0$ dan $f(x)=2x-5$ voor $x\le4\frac{1}{2}$
ii Als $9-2x\lt0$ dan $f(x)=-2x+13$ voor $x\gt4\frac{1}{2}$

...maar dat geldt alleen voor $x\ge3$

Bij B. kan je dan weer twee gevallen onderscheiden:

i. Als $-3+2x\ge0$ dan $f(x)=-2x+7$ voor $x\ge1\frac{1}{2}$
ii. Als $-3+2x\lt0$ dan $f(x)=2x+1$ voor $x\lt1\frac{1}{2}$

...maar dat geldt alleen voor $x\lt3$

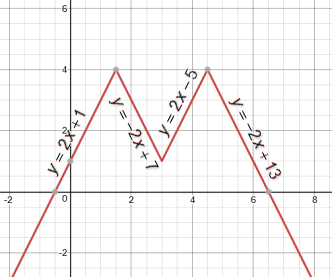
Meer moet het niet zijn...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 11 juli 2016