|
|
|
\require{AMSmath}



4 kleine vraagjes
Hallo,
Ik heb 4 kleine vraagjes over oplossen van vergelijkingen:
vraagje 1:
bij het oplossen v.e. bep vergelijking moet je op een gegeven moment (5/2) delen door a. In mijn boek maken ze daar dan van: = 5/2a
Mag dat zo? Is daar net zo'n regel voor als wanneer je (5/2)*a hebt, dat je dan 5a/2 krijgt; dus die a alleen op de bovenste regel? En dus als je gedeeld door doet dat de a op de onderste regel komt?
vraagje 2:
Je hebt: -(2/a2)=0,8
De min hoort dus zowel bij de onderkant als de bovenkant, dus -(2/a2)=(-2/a2) en -(2/a2)= (2/-a2)
Klopt dat?
Dus in feite hoort die min dan dus ook bij de onderkant, is het dan:
-2=0,8/a2 of 2=0,8/-a2 dus dat je die min meeneemt bij het delen, omdat hij ook bij de onderkant hoort?
vraagje 3:
1-(2/a3)= 0
is dat gelijk aan: 1=(2/a3)
of mag dat niet omdat er eigenlijk staat -1*(2/a3)?
vraagje 4:
Je moet oplossen:
a+(1/a2)=0
het antwboek geeft als oplossing
a3=-1 en a=-1(vervalt)
ikzelf krijg er andere antwoorden uit
willen jullie stap voor stap uitleggen hoe ze hier zo uitkomen?
en je moet oplossen:
1-2a^-3=0
het antwboek geeft als oplossing
a3=2 en a=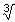 2 2
ikzelf krijg er andere antwoorden uit
willen jullie stap voor stap uitleggen hoe ze hier zo uitkomen?
Dat waren mijn vraagjes dan
Alvast hartstikke bedankt voor het beantwoorden!
Groetjes Anne
Anne
Leerling bovenbouw havo-vwo - zondag 2 maart 2003
Antwoord
vraagje 1:
bij het oplossen v.e. bep vergelijking moet je op een gegeven moment (5/2) delen door a. In mijn boek maken ze daar dan van: = 5/2a
Zie het als twee breuken, dan kan het niet fout:
Delen door a is hetzelfde als vermenigvuldigen met 1/a
Wanneer je nu 5/2 deelt door a dan is dat hetzelfde als
5/2·1/a=5/2a
(Als je twee breuken VERMENIGVULDIGT mag je teller en noemer apart vermenigvuldigen)
Zo is a hetzelfde als a/1 dus is 5/2·a= 5/2·a/1 =5a/2
vraagje 2:
Je hebt: -(2/a2)=0,8
De min hoort dus zowel bij de onderkant als de bovenkant...
Zo moet je dat dus niet zien want dan loop je het gevaar om die min ook zowel bij de onderkant als de bovenkant neer te zetten. Die min geeft aan dat je het tegengestelde van (2/a2) moet hebben en dat kan je krijgen door vervolgens die min ofwel bij de teller (boven) ofwel bij de noemer erbij te zetten. Dat doe je dan wel goed .......
vraagje 3:
1-(2/a3)= 0
is dat gelijk aan: 1=(2/a3)
Yep: Terug naar de basis: in een vergelijking mag je aan beide kanten van het = teken 2/a3 optellen. Dan staat het er al.
vraagje 4:
Je moet oplossen:
a+(1/a2)=0 $\Leftrightarrow$ a = -1/a2 $\Leftrightarrow$ (aan beide kanten met a2 vermenigvuldigen)
a3=-1 $\Leftrightarrow$ a=-1 (waarom die moet vervallen is mij een raadsel)
en je moet oplossen: 1-2a-3=0
Zelfde truc eerst het gedeelte met die a-3 naar links en dan aan beide kanten vermenigvuldigen met a3
Zelf proberen !
Met vriendelijke groet
JaDeX

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 3 maart 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








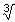 2
2
