WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Cyclometrische functies oefening

Beste

Zou u me alstublieft kunnen helpen met de volgende oefening?
sin(2·Bgtan(1/2))=?
Ik begin met hiervan 2·sin(Bgtan(1/2))·cos(Bgtan(1/2)) te maken en daarna de Bgtan(1/2) te vervangen door Bgsin(1/2)/Bgcos(1/2), maar dan weet ik niet meer wat ik moet doen. Wanneer ik dat laatste uitwerk, zit ik helemaal vast...

Vriendelijke groeten en alvast bedankt!!
Em
3de graad ASO - zondag 17 april 2016

Antwoord

Allereerst: Bgtan(1/2) is niet gelijk aan Bgsin(1/2)/Bgcos(1/2)! Je bent in de war met de 'gewone' sinus, cosinus en tangens.

Ik zou deze opgave als volgt aanpakken:

Bgtan(1/2) is de hoek waarvan de tangens gelijk is aan 1/2. In een rechthoekige driehoek ziet dat er zo uit:

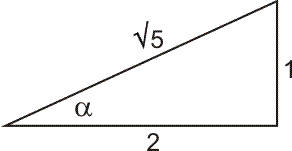
In deze figuur is $\alpha$=Bgtan(1/2).

Met Pythagoras bereken je de schuine zijde. Je ziet dan ook wat sin($\alpha$) en cos($\alpha$) zijn, hiermee bereken je 2·sin($\alpha$)·cos($\alpha$).

OK zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 17 april 2016