|
|
|
\require{AMSmath}



Pappus
Beste meneer/mevrouw,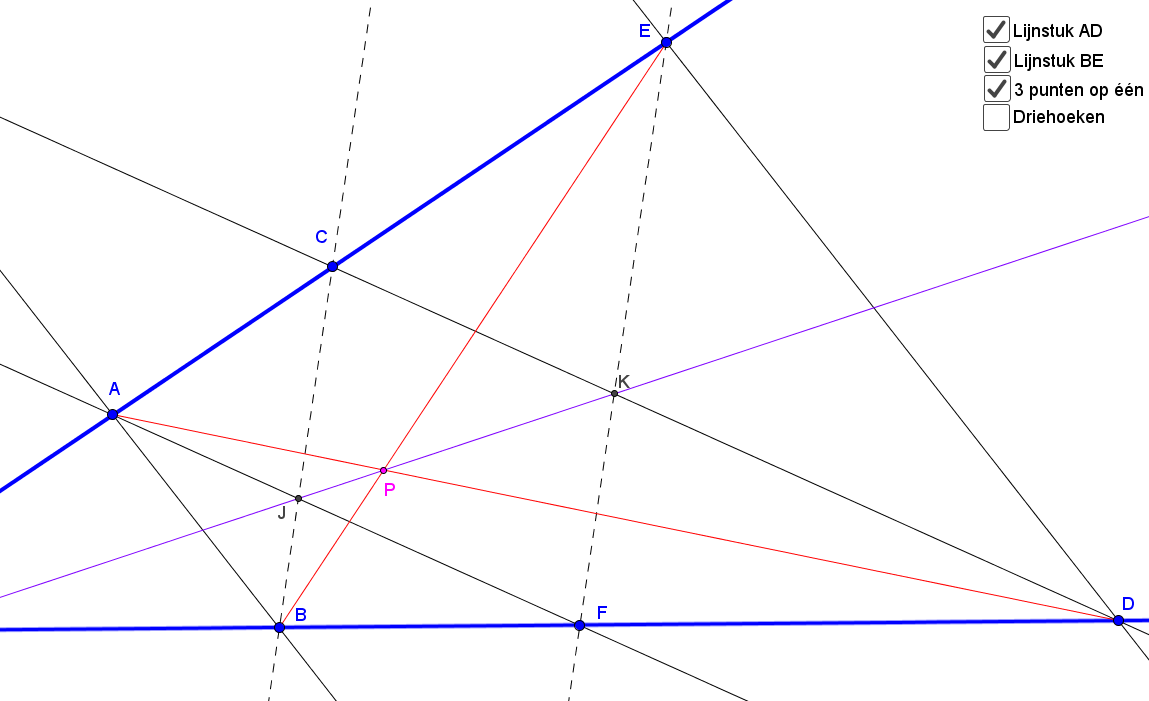
In de afbeelding is gegeven AB//ED en CD//AF. Te bewijzen dat CB//EF. Ik vind het ontzettend lastig om de juiste driehoeken hierbij te zoeken. Kunt u me op weg helpen?
Koen
Student hbo - donderdag 3 maart 2016
Antwoord
Hallo Koen,
Ik dacht aan het volgende:
- Vanwege $AB$//$ED$ hebben we $\Delta ABP \sim \Delta DEP$;
- Vanwege $AF$//$CD$ hebben we $\Delta AJP \sim \Delta DKP$.
De zijden van beide paren driehoeken hebben dezelfde verhouding, want $AP$ en $DP$ zijn in beide gevallen overeenkomende zijden. Dus $JP : KP = BP : EP$.
Ook geldt $\angle BPJ = \angle EPK$ (overstaande hoeken). Derhalve $\Delta BPJ \sim \Delta EPK$, (twee zijden in gelijke verhouding met gelijke ingesloten hoek - zhz).
En nu ben je dicht bij een compleet bewijs. Zie je waarom?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 5 maart 2016
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










