WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Oppervlakte van een prisma

Dit is een reactie op vraag 77250

Sorry het lukt niet. Ik heb op uw site een andere manier gevonden om de oppervlakte te berekenen van een achthoek show3archive.asp?id=2662&j=2002 Ik heb de oppervlakte berekend met behulp van goniometrie. Ik heb hierbij voor lijnstuk AB de waarde 'x' genomen en heb met behulp van de tangens de oppervlakte van de achthoek kunnen berekenen. Dit kwam (afgerond) uiteindelijk op een waarde van 4,83x². Ik heb gekeken naar uw berekening van de minimale oppervlakte van een prisma. show3archive.asp?id=1594 Ik heb nu dus de inhoud (1 liter) en de oppervlakte van het grondvlak G(4,83x²). Ik begrijp echter niet wat u doet vanaf de stap 'ik ga nu de oppervlakte uitdrukken in 'r''. Het lijkt erop alsof u opnieuw de oppervlakte van grondvlak G berekent, terwijl deze toch al bekend is. Daarvóór staat er namelijk 'G = ¹/₄ · r² · 'wortel van 3'. Kunt u de stappen uitleggen die u maakt? Ik kan ze namelijk niet toepassen op mijn prisma.
Alvast heel erg bedankt!
Lisa
Leerling bovenbouw havo-vwo - zondag 3 januari 2016

Antwoord

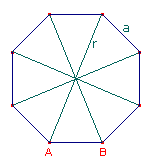Het idee is om de oppervlakte van het prisma uit te drukken in 'x' (de lengte AB). Noem de oppervlakte van het grondvlak even G. Er geldt:

Inhoud = G·h
Oppervlakte = 2·G + 8·x·h

Daarvoor ga je de oppervlakte G uitdrukken in 'x'.

G = ...x...

Dan ga je met de inhoudsformule ook 'h' uitdrukken in 'x'. Je weet immers van de inhoud 1 liter is. Uiteindelijk krijg je een functie voor de oppervlakte van het prima uitgedrukt in 'x'. Dan kun je gaan differentiëren om het minimum te bepalen. Dat is het idee!

Lukt dat dan?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 3 januari 2016