WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Formule centripetale versnelling berekenen

Dit is een reactie op vraag 77255

Ik snap het denk ik. Maar ik vind het voorbeeld een klein beetje verwarrend. Je weet alleen dat (g=gemiddeld, i=instantaan) v_g = ∆s/∆t en dat v_p = ds/dt. In het voorbeeld geef jij de formule s = t² als voorbeeld, maar deze formule is slechts een voorbeeld. Je weet dus eigenlijk alleen dat v_p = ds/dt.

Ik heb iets bedacht waardoor ik het misschien meer snap, maar ik weet niet zeker of dit wel een goed voorbeeld is.
Ik weet niet precies hoe ik een afbeelding in mijn vraag krijg, maar het gaat over deze afbeelding:

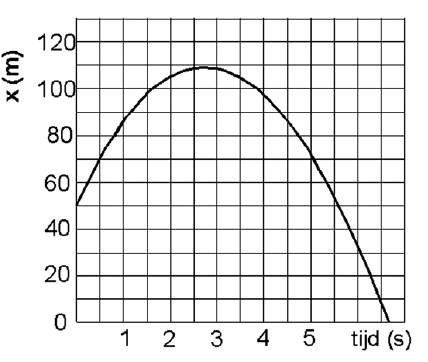
In deze afbeelding zie je een grafiek met op de horizontale as de tijd (t) en op de verticale as de afstand (x). Als ik een willekeurig klein interval ∆t neem, is de grootte van ∆x bepaald. Bijvoorbeeld in het interval t=0 tot t=5 is ∆t=5 (=5-0) en ∆x=20 (=70-50). Dit betekent dus dat, als ∆t steeds kleiner wordt (lim ∆t→0), dan wordt ∆x ook steeds kleiner.

Ik snapte jouw voorbeeld niet helemaal, omdat je normaal gesproken jouw voorbeeldformule niet kent, maar is dit ook een goed voorbeeld waarmee je kan aantonen dat als ∆t kleiner wordt, dit ook voor ∆x geldt?

En als je een willekeurig klein interval ∆s kiest, is ∆t ook bepaald, dus maakt het uit of je de formule van 'de' snelheid op een bepaald moment zo schrijft: v = lim ∆t→0 ∆s/∆t of zo: v = lim ∆s→0 ∆s/∆t ?

Kun je misschien jouw voorbeeld uitleggen zonder een extra-gegeven formule (je gebruikte nu s = t² als voorbeeld), want dit vond ik dus een beetje verwarrend, en kun je misschien beoordelen of mijn voorbeeld ook goed is?

Bedankt voor alle hulp!
135455
Leerling onderbouw vmbo-havo-vwo - woensdag 30 december 2015

Antwoord

Allereerst: op het interval t=0 tot t=5 in jouw voorbeeld is ∆x=-20. De waarde van x is met 20 afgenomen, niet toegenomen.

Verder is jouw voorbeeld goed: het maakt niet uit of je waarden van t en x uit een formule haalt, uit een tabel of uit een grafiek. Bij een grafiek zit je natuurlijk wel met een beperkte nauwkeurigheid van aflezen, maar een tabel of grafiek kan ook het resultaat zijn van metingen met beperkte nauwkeurigheid. In beide gevallen is de nauwkeurigheid van de berekende snelheden dan ook beperkt.

Als illustratie heb ik nog eens een willekeurig punt A in jouw grafiek genomen, en 3 punten B₁, B₂ en B₃ op een steeds kleinere afstand ∆t vanaf A, zie hieronder.

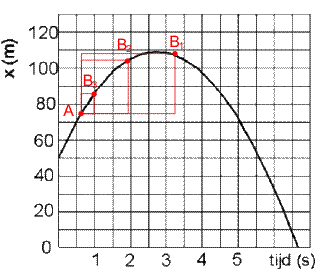
De horizontale afmeting van de rechthoekjes geven ∆t weer, de verticale afmeting de bijbehorende ∆x. Je ziet dat ∆x naar nul gaat wanneer ∆t naar nul gaat. Zolang de curve geen sprongen of openingen bevat, of verticale stukken, kan dit niet anders: bij een smaller rechthoekje hoort automatisch een lager rechthoekje. In de werkelijke wereld komen geen sprongen of verticale stukken voor, omdat een voorwerp niet op twee plaatsen tegelijk kan zijn en niet op een bepaalde plaats kan verdwijnen om op een andere plaats weer te verschijnen.

Tot slot nog even over het verschil tussen lim ∆t→0 en lim ∆s→0. Het doel is om 'de' snelheid te bepalen op een bepaald tijdstip t. Hiervoor bepaal je de gemiddelde snelheid op een klein tijdsinterval ∆t, en maak je de benadering steeds beter door dit interval oneindig kort te maken. De tijd t is dus de onafhankelijke variabele, je neemt lim ∆t→0 om het effect hiervan op s en/of v te bepalen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 31 december 2015