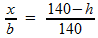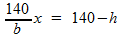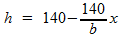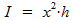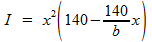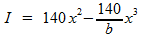|
|
|
\require{AMSmath}



Balk in piramide met een regelmatig achthoekig grondvlak
Er is een regelmatig achthoekige piramide, met zijdes van 60 cm. De hoogte h van de piramide bedraagt 140 cm. In de piramide wordt een balk geplaatst met lengte en breedte x centimeter en hoogte h centimeter.- Wat zijn de maximale maten van x en h waarvan de balk in de piramide past en wat is de inhoud van die balk met deze waarde van x en h?
Bjorn
Leerling bovenbouw havo-vwo - donderdag 5 november 2015
Antwoord
Hallo Bjorn,
Hieronder heb ik het bovenaanzicht en het vooraanzicht van de piramide getekend, met daarin de grijze balk.
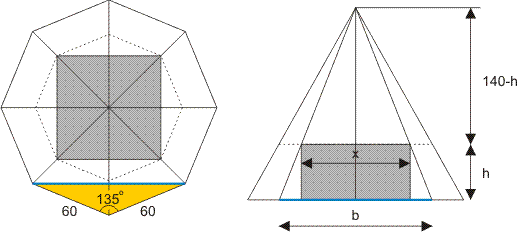
In de figuur rechts zie je:
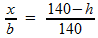
Het blauwe lijnstuk b is een diagonaal van de achthoek, evenwijdig aan een zijde van de balk, zie ook de figuur links.
In deze formule isoleren we h:
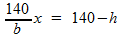
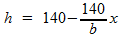
Voor de inhoud I van de balk geldt:
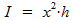
dus:
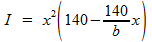
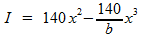
De waarde van b kan je berekenen met behulp van de cosinusregel, toegepast op het gele driehoekje in de linker figuur. Je hebt dan de inhoud I als functie van x. De waarde van x waarbij I maximaal wordt, vind je door de afgeleide van deze functie gelijk te stellen aan nul. Met deze waarde kan je ook de maximale inhoud berekenen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 6 november 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|