WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Steekproef en significantie

Een steekproef is geselecteerd uit een normale populatie met gemiddelde = 40 en een standaardafwijking = 10. Na de behandeling behandeling is een M=42 gevonden.

a. hoe groot moet de steekproef zijn voor deze steekproef gemiddelde om significant te zijn. neem aan dat het een tweezijdige toets is met alfa niveau 0.05

Ik heb deze vraag al eerder gesteld, maar ik heb geen goed antwoord gekregen. Het is waarschijnlijk wel duidelijk uitgelegd maar ik snap het gewoon niet.
Statistiek en kansrekenen

yalda
Student universiteit - woensdag 28 oktober 2015

Antwoord

Hallo Yalda,

Ik zal proberen in kleine stapjes uit te leggen wat er nu eigenlijk gebeurt.

Het gemiddelde van je steekproef is 42. Dat wil niet zeggen dat het gemiddelde van de gehele populatie ook 42 is. Misschien heb je een ongelukkige steekproef getrokken en is het werkelijke gemiddelde van de populatie 43 of 44, dan heeft de behandeling beter geholpen dan je uit de steekproef zou denken. Maar het kan ook zijn dat het werkelijke gemiddelde van de gehele populatie 41 is (dan heeft de behandeling maar een beetje geholpen) of zelfs 40 (dan heeft de behandeling geen enkel effect).

De vraag is dus:
Is de toename van 40 naar 42 groot genoeg om aan te nemen dat de behandeling effect heeft gehad? We noemen dit: is de toename van 40 naar 42 significant?

De denkwijze is nu als volgt:
Laten we eens aannemen dat de behandeling geen effect heeft gehad. Dit is de nul-hypothese: we nemen aan dat de verandering nul is, het gemiddelde van de populatie is nog steeds 40. Wanneer we dan steekproeven nemen, zal het gemiddelde van deze steekproeven niet altijd precies 40 zijn. De ene keer vinden we door toeval een wat lager gemiddelde, de volgende keer misschien weer een wat hoger gemiddelde.

De verdeling van onze gevonden gemiddelde waarden ziet er bijvoorbeeld zo uit:

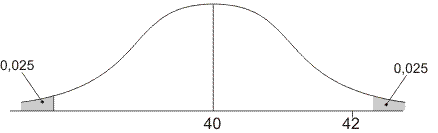
De kans dat we, puur door toeval, een gemiddelde waarde vinden in de grijze gebiedjes is 5%. In dit voorbeeld ligt de waarde 42 nog in het witte gebied. Dat betekent dat de kans meer dan 5% is dat we zo'n verschil van 2 (of groter) vinden. Dan noemen we het gevonden verschil niet significant. we weten niet of de 'verbetering' van 2 door toeval komt of door een geslaagde behandeling.

De verdeling van onze gevonden gemiddelden kan er ook zo uitzien:

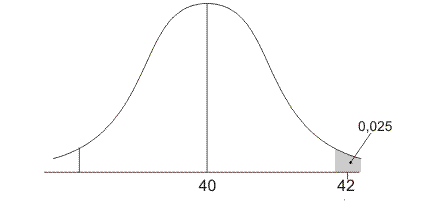
Deze verdeling heeft een kleinere standaardafwijking, hierdoor is de klokvorm smaller. Nu ligt de waarde 42 in de grijze gebiedjes. Dit betekent dat, als er in werkelijkheid geen effect zou zijn (werkelijk gemiddelde is 40), we minder dan 5% kans hebben dat we zo'n verschil van 2 of meer vinden. Maar we hebben het wel gevonden! Dan nemen we aan dat dit geen toeval is, en nemen aan dat de behandeling toch wel effect heeft gehad. We noemen het verschil dan wel significant.

Onderstaande figuur geeft de grens aan tussen wel significant en niet significant:

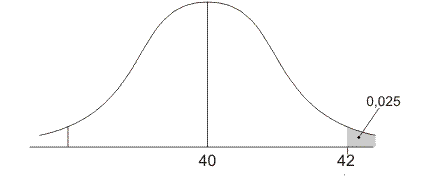
Hier is de standaardafwijking zodanig dat de waarde 42 precies op de grens ligt tussen het witte en grijze gebied.

Kortom:
Als de standaardafwijking te groot is, komt onze gevonden waarde in het witte gebied en noemen we het verschil niet significant.
Als de standaardafwijking klein genoeg is, komt onze gevonden waarde in het grijze gebied en noemen we het verschil wel significant
Nu gaan we berekenen welke waarde van de standaardafwijking hoort bij de derde figuur. De oppervlakte rechts van 42 is 0,025, dus links van deze grens is de oppervlakte 0,975. In de tabel voor Z-scores zoeken we de Z-score op die hoort bij deze oppervlakte. We vinden:

Z=1.96

We gebruiken de formule:

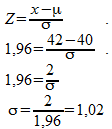
Bedenk nu nog een keer over welke standaardafwijking we het nu steeds hebben: de standaardafwijking van gemiddelde waarden, deze zouden we 'zien' wanneer we een heleboel steekproeven zouden nemen en steeds de gemiddelde waarde berekenen. Deze standaardafwijking kunnen we zelf beïnvloeden met de grootte van de steekproef: hoe groter de steekproef, hoe dichter gemiddelde waarden bij elkaar liggen bij herhaling van de steekproef, en dus hoe kleiner de standaardafwijking van deze gemiddelde waarden. Hiervoor hebben we deze formule:

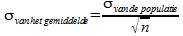
De standaardafwijking van de populatie is 10. We moeten de steekproefgrootte n nu zodanig kiezen dat de standaardafwijking van het gemiddelde 1,02 wordt:

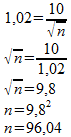
Officieel moet je naar boven afronden, omdat n=96 net iets te weinig zou zijn. We vinden dus: n minimaal 97.

Hopelijk is het nu wel duidelijk. Zo niet, stel dan weer gerust een vervolgvraag, maar het is dan wel handig om aan te geven wat je wel begrijpt en vanaf welk punt het niet meer duidelijk is. Dan kunnen we ons antwoord beter afstemmen op jouw probleem.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 29 oktober 2015

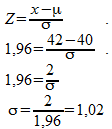
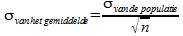
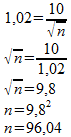
Re: Steekproef en significantie