WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Re: Kansen: leerlingen op excursie

Dit is een reactie op vraag 76434

Er zitten in totaal 30 lln in de klas. Er mogen 10 lln niet mee. In totaal kunnen dus 20 lln mee. Ik wil 1 lln kiezen die wel mee mag. De combinatie is dan 20ncr1.

Bij P(0 leerlingen) = 20ncr0
Arif M
Leerling bovenbouw havo-vwo - woensdag 30 september 2015

Antwoord

Arif, je werkt te slordig. Heb je de vraag nog wel even gelezen voordat je antwoord gaf?
Hoeveel leerlingen worden door de mentor aangewezen? Hoeveel van deze leerlingen moeten uit de groep komen die wel mee mogen, en hoeveel van deze leerlingen moeten uit de groep komen die niet mee mogen?

Tip: de formulering is soms best ingewikkeld. Maak het eenvoudiger door de leerlingen voor te stellen als gekleurde knikkers, bijvoorbeeld:

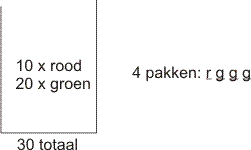
30 leerlingen totaal, dus: 30 knikkers
10 leerlingen die niet mee mogen: 10 knikkers zijn rood
20 leerlingen die wel mee mogen: 20 knikkers zijn groen.

De mentor wijst 4 leerlingen aan: pakt dus 4 knikkers.

Maak hiervan een schets:

Dan gaan we de vraag nog eens goed lezen. Wat bedoelen we ook alweer met P(1 leerling)? Dat was: 1 leerling die niet mee mag. Dus: je moet 1 rode knikker pakken:

In totaal moeten er 4 knikkers worden gepakt. Wat komt er dus op de andere 3 plekken in de schets? Juist: groen!

Nu ga je de combinaties opstellen boven de breukstreep:
- Hoeveel rode knikkers moet je pakken?
- Uit hoeveel rode knikkers kan je kiezen?

- Hoeveel groene knikkers moet je pakken?
- Uit hoeveel groene knikkers kan je kiezen

Hiermee ga je door tot je alle kleuren hebt gehad die gepakt moeten worden. In dit geval zijn er maar twee kleuren.

Dan de combinatie onder de breukstreep:
- Hoeveel knikkers moet je in totaal pakken?
- Uit hoeveel knikkers kan je in totaal kiezen?

Volg dit stappenplan nauwkeurig, dan kan het haast niet mis gaan.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 30 september 2015

Re: Re: Re: Re: Re: Kansen: leerlingen op excursie