WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

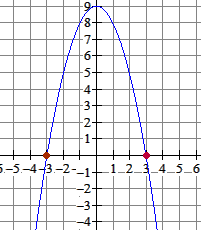
Domein en bereik

Als je van deze formule het bereik moet bepalen zonder rekenmachine lukt dit mij niet om dat dan geen max kunt zien.
f(x)=log(9-x²)
Hoe doe je dit dan?
Domein en bereik

amasja
Leerling bovenbouw havo-vwo - vrijdag 25 september 2015

Antwoord

Als je naar $g(x)=-x^2+9$ kijkt dan ziet dat er zo uit:

De functie $f$ bestaat alleen als $g(x)\gt0$, dus $-3\lt x \lt3$. Bovendien is $f(x)$ maximaal als $g(x)$ maximaal is en dat is dan bij $x=0$.

$f(x)=\log(9-0^2)=\log(9)$, dus het maximum van $g$ is $\log(9)$

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 25 september 2015