WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Twee halve parabolen

Hoi,

Ik moet de exacte oppervlakte tussen 2 parabolen en een lijn algebraïsch berekenen.

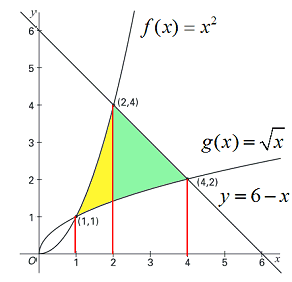
Dit is de opgave (het gaat om 18):
Twee halve parabolen
Dit is de uitwerking (18 staat helemaal onderaan):
Uitwerking
Ik begrijp de eerste drie stappen, maar als ik dan 2 - 1 als x invul bij de eerste primitieve, en 4 - 2 als x bij de tweede primitieve, dan loop ik vast. De stap tussen 2/3 en 4 begrijp ik dus niet. Kunt u me hiermee helpen?
Integreren

tijl
Leerling bovenbouw havo-vwo - zondag 21 juni 2015

Antwoord

$
\eqalign{
& \int\limits_{x = 1}^2 {x^2 - \sqrt x } \,\,dx + \int\limits_{x = 2}^4 {6 - x - \sqrt x } \,\,dx \cr
& \left[ {\frac{1}
{3}x^3 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 1}^2 + \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 \cr
& I. \cr
& \left[ {\frac{1}
{3}x^3 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 1}^2 = \frac{1}
{3} \cdot 2^3 - \frac{2}
{3} \cdot 2^{\frac{3}
{2}} - \left( {\frac{1}
{3} \cdot 1^3 - \frac{2}
{3} \cdot 1^{\frac{3}
{2}} } \right) \cr
& \left[ {\frac{1}
{3}x^3 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 1}^2 = \frac{8}
{3} - \frac{4}
{3}\sqrt 2 - \left( {\frac{1}
{3} - \frac{2}
{3}} \right) \cr
& \left[ {\frac{1}
{3}x^3 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 1}^2 = \frac{8}
{3} - \frac{4}
{3}\sqrt 2 + \frac{1}
{3} \cr
& \left[ {\frac{1}
{3}x^3 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 1}^2 = 3 - \frac{4}
{3}\sqrt 2 \cr
& II. \cr
& \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 = 6 \cdot 4 - \frac{1}
{2} \cdot 4^2 - \frac{2}
{3} \cdot 4^{\frac{3}
{2}} - \left( {6 \cdot 2 - \frac{1}
{2} \cdot 2^2 - \frac{2}
{3} \cdot 2^{\frac{3}
{2}} } \right) \cr
& \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 = 24 - 8 - \frac{{16}}
{3} - \left( {12 - 2 - \frac{4}
{3}\sqrt 2 } \right) \cr
& \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 = 10\frac{2}
{3} - \left( {10 - \frac{4}
{3}\sqrt 2 } \right) \cr
& \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 = 10\frac{2}
{3} - 10 + \frac{4}
{3}\sqrt 2 \cr
& \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 = \frac{2}
{3} + \frac{4}
{3}\sqrt 2 \cr
& III. \cr
& \left[ {\frac{1}
{3}x^3 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 1}^2 + \left[ {6x - \frac{1}
{2}x^2 - \frac{2}
{3}x^{\frac{3}
{2}} } \right]_{x = 2}^4 = 3 - \frac{4}
{3}\sqrt 2 + \frac{2}
{3} + \frac{4}
{3}\sqrt 2 = 3\frac{2}
{3} \cr}
$

Als je uitwerkingen zoekt van eindexamens dan kan je ook 's kijken op:
EXAMENS NIEUWE STIJL met uitwerkingen

Zie wiskunde B1, vwo in 2004

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 21 juni 2015