|
|
|
\require{AMSmath}



Omtrek van twee figuren dat samen 90 is
Hallo,
Bij een opdracht kom ik niet echt uit.
Er worden twee figuren gegeven waarvan figuur a een soort zaklamp is met aan de linkerkant de steel en de zijde is 1. De twee 'lange' zijden van de zaklamp zijn aan elke zijde 3. Dan volgt de trapezium waarvan beide schuine zijden p is. En dan de platte zijde van de trapezium die 3 is.
Figuur b is een trapezium waarvan de bovenste zijde 2 is en de onderste zijde 4. De schuine zijden zijn allebei k.
Er staat er dan onder:
Stel, de omtrek van figuur a is tweemaal zo groot als de omtrek van figuur b. Stel, samen zijn ze 90. Bereken dan p en k.
Souray
Leerling bovenbouw havo-vwo - zondag 7 juni 2015
Antwoord
Eerst maar 's een tekening:
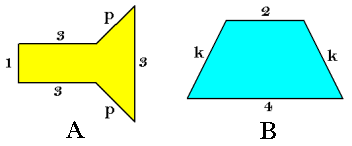
De omtrek van de linker figuur is gelijk aan $2p+10$.
De omtrek van de rechter figuur is gelijk aan $2k+6$.
Er geldt;
$2p+10=2·(2k+6)$
$2p+10+2k+6=90$
Je hebt dan een stelsel van twee vergelijkingen met twee onbekenden en als je dat oplost van ben je er uit.
$2p+10=4k+12$
$2p+2k+16=90$
$2p-4k=2$
$2p+2k=74$
$p-2k=1$ (1)
$p+k=37$ (2)
Als je nu (2)-(1) neemt dan krijg je:
$3k=36$
$k=12$ en $p=25$
Zo'n stelsel van vergelijkingen bedenken en oplossen is wel een handige aanpak. Helpt dat?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 7 juni 2015
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










