WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Periode sinusfunctie bepalen

Hallo,
Bij het bepalen van een sinusfunctie heb ik dit geleerd:
f(x) = d + a · sin(b(x-c) waarbij geldt:
d: verschuiving van de evenwichtsstand
a: vermenigvuldiging t.o.v. de x-as (veranderen van amplitude)
b: vermenigvuldiging t.o.v. de y-as (periode)
c: verschuiving over de x-as

Nu heb ik geleerd dat de periode uit de formule bepaald kan worden, namelijk door b. periode = 2$\pi$/ b

Nu heb ik een probleem. In mijn lesboek staat een opgave met deze twee sinusfuncties:
f(x)= sin³(x) en g(x) = sin⁴(x)
Er wordt gevraagd wat de periode van elk van de functies is. Nu blijkt de periode van functie f 2$\pi$ te zijn en de periode van functie g 1$\pi$. Hoe kun je dit weten? Er is namelijk geen 'b', zodat je de periode kan berekenen. Kun je er enkel achter komen door de grafiek te plotten op de grafische rekenmachine?

met vriendelijke groet,

Nina
Leerling bovenbouw havo-vwo - zaterdag 25 april 2015

Antwoord

Hallo Nina,

Met behulp van een plot op je rekenmachine krijg je snel een vermoeden wat de periode moet zijn, maar in het algemeen levert zo'n plotje benaderingen. Om de periode echt vast te stellen, moet je inderdaad een beetje doordenken en wiskundig inzicht gebruiken.

Bedenk dat je sin³(x) kunt schrijven als sin²(x)·sin(x), en sin⁴(x) als (sin²(x))². Laten we dan eens bekijken wat de periode is van sin²(x). Dat kan op twee manieren:

1) Aan de hand van formules
Je hebt misschien deze formule geleerd:

cos(2x) = 1-2sin²(x)
(ook: cos(2x) = cos²(x)-sin²(x) = 2cos²(x)-1, maar aan deze vormen hebben we nu even niks).

Hiermee kan je sin²(x) herleiden tot:

sin²(x) = ¹/₂ - ¹/₂cos(2x)

De periode van sin²(x) is dus hetzelfde als de periode van cos(2x), de periode van sin²(x) is dus $\pi$.

2. Aan de hand van de grafiek van de sinusfunctie
Hieronder zie je de grafiek van de sinusfunctie (doorgetrokken lijn):

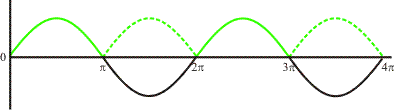
Wanneer we gaan kwadrateren, dan leveren negatieve delen van de grafiek (bijvoorbeeld tussen $\pi$ en 2$\pi$) hetzelfde resultaat op als wanneer deze delen positief waren geweest (groene stippellijn). Je kunt dus net zo goed de groene curve kwadrateren. Je weet dat de negatieve delen prcies dezelfde vorm hebben als de positieve delen, de groene curve heeft dus een periode van 1·$\pi$. Je weet dus van tevoren dat de curve na kwadrateren ook een periode van $\pi$ zal hebben.

Nu we weten dat de periode van sin²(x) gelijk is aan $\pi$, gaan we beredeneren wat dit betekent voor f(x) en g(x) uit jouw vraag:

Bij f(x) vermenigvuldig je sin²(x) met sin(x). Het eerste deel herhaalt na periodetijd $\pi$, maar het tweede deel herhaalt pas na periodetijd 2$\pi$. Het totaal herhaalt dan ook pas na periodetijd 2$\pi$.

Bij g(x) kwadrateer je sin²(x). De functie sin²(x) herhaalt na periodetijd $\pi$, dat verandert niet door kwadrateren: ook sin⁴(x) herhaalt zodoende na periodetijd $\pi$.

Is het hiermee duidelijker geworden waarom de periodetijden zijn zoals deze zijn?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 25 april 2015

Re: Periode sinusfunctie bepalen