WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Spelen met een revolver

Ik heb een wiskundige vraag die ik niet opgelost krijg.

Een man 'speelt' met een revolver met 6 kamers. In één van die kamers zit een kogel. Hij waagt 4 pogingen. Bereken de kans dat hij het niet overleeft.

Ik snap echt niet hoe ik een kansboom moet maken of of ik het anders kan oplossen...

Alsvast bedankt!
Vtgl
2de graad ASO - zondag 1 februari 2015

Antwoord

Ik ga er vanuit dat bij elke poging de kans op 'geladen' steeds $\frac{1}{6}$ is (met terugleggen). Hij doet 4 pogingen. De kans dat het de eerste keer mis gaat is $\frac{1}{6}$. De kans dat het de eerste keer goed gaat is $\frac{5}{6}$.

Als het de eerste keer goed gaat dan is de kans dat het de tweede keer fout gaat gelijk aan $\frac{5}{6}\cdot\frac{1}{6}$. De kans dat het ook de tweede keer goed gaat is $\frac{5}{6}\cdot\frac{5}{6}$.

En zo verder, al met al kortom:

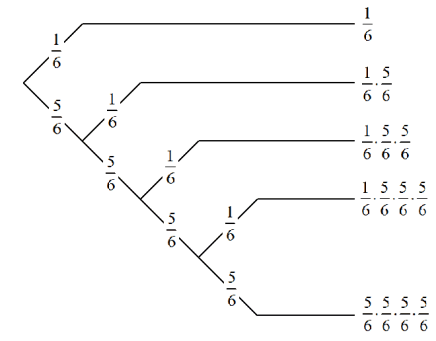
P(na 1 keer fout)=$\frac{1}{6}$
P(na 2 keer fout)=$\frac{5}{6}\cdot\frac{1}{6}$
P(na 3 keer fout)=$\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}$
P(na 4 keer fout)=$\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}$

Als je deze 4 kansen optelt weet je de kans dat hij het niet overleeft.

Naschrift

Een andere redenering zou kunnen zijn dat je zegt dat je, als je dit wilt overleven, je 4 keer achter elkaar 'niet geladen' moet hebben. De kans daarom is $(\frac{5}{6})^{4}$. De kans om het niet te overleven is dan gelijk aan de complementaire kans $1-(\frac{5}{6})^{4}$. Daar komt dan precies hetzelfde uit als hierboven.

Meer in 't algemeen

$
\eqalign{\sum\limits_{k = 1}^n {\frac{1}
{6} \cdot \left( {\frac{5}
{6}} \right)^{k - 1} } = 1 - \left( {\frac{5}
{6}} \right)^n}
$

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 1 februari 2015