WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ligging van een pijpleiding

Ik zit met een opgave die maar niet lukt. Ik heb gisteren al heel de dag geprobeerd maar geraak er niet uit.

Opgave: Om reparaties aan een pijpleiding uit te voeren vanuit een vast punt O op de begane grond, voert men metingen uit om de ligging van de pijpleiding te bepalen. Ten opzichte van een assenstelsel door O met x-as en y-as langs het grondoppervlak en de z-as daar loodrecht op, vindt men twee punten A(0, 15, -32) en B(20, 20, -30). Bepaal de coördinaat van het punt P op de pijpleiding dat het dichtste bij O ligt. (Verwaarloos de diameter van de pijpleiding; met andere woorden veronderstel dat de punten A, B en P op een rechte liggen.)

Dit moet opgelost worden met vectoren. Ik heb o.a. al de vector AB=20i+5j+2k, de vector OP heb ik voorgesteld als OP=xi+yj+zk. Ik weet dat AB . OP = 0, omdat wanneer deze vectoren loodrecht op elkaar staan, de afstand het kortst is. Ik heb ook de hoek OBA, BOP, BOA en POA berekend maar weet eigenlijk niet als dit nodig was.
Kan iemand mij helpen met deze opgave en een duidelijk stappenplan geven?

Jasper
Jasper
3de graad ASO - zondag 25 januari 2015

Antwoord

Hallo Jasper,

Punt P ligt ergens op de pijplijding. De vector OP wijst dus een punt op de leiding aan.
De vectorvergelijking van de pijpleiding wordt gegeven door een willekeurige plaatsvector van een punt op deze leiding (neem bijvoorbeeld punt A) en de richtingsvector (B-A), dus:

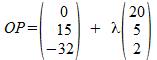
Deze vector OP moet loodrecht staan op de richtingsvector van de pijpleiding, dus het inwendig product moet nul zijn:

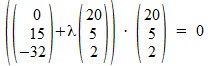
Wanneer je de haakjes netjes wegwerkt, zou dit een vergelijking moeten opleveren waarmee l is te berekenen. Dan is de vector OP bekend, dus ook punt P op de leiding.

Kan je hiermee verder?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 25 januari 2015

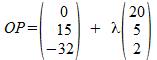
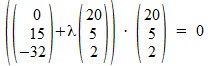
Re: Ligging van een pijpleiding