WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Kwadratische problemen

Dit is een reactie op vraag 74382

Wat moet ik dan met de -0,5 doen? Want ik begrijp het nog steeds niet echt. En ik begrijp maar half wat u bedoelt in uw antwoord. Zou u het misschien makkelijker kunnen uitleggen voor mij?

Groetjes Cher.
Cher
Leerling onderbouw vmbo-havo-vwo - zondag 23 november 2014

Antwoord

Je wilt weten voor welke waarde(n) van $x$ de $f(x)$ gelijk is aan nul.

Gegeven: $f(x)=-0,5(x+2)(x-6)$

Als je $f(-2)$ uitrekent dan vul je $x=-2$ in. Dan staat er:
$f(-2)=-0,5(-2+2)(-2-6)=-0,5·0·-8=0$
Er komt dan $0$ uit. Waarom? Omdat $x+2$ dan nul wordt en dan komt er $0$ uit.

Er is nog een mogelijkheid. Neem $x=6$ dan staat er:
$f(6)=-0,5(6+2)(6-6)=-0,5·8·0=0$
Er komt dan ook $0$ uit. Waarom? Omdat dan $x-6$ nul wordt.

De snijpunten met de $x$-as (daar waar $f(x)$ nul is!) zijn dus:
$A(-2,0)$ en $B(6,0)$

We noemen dat wel de nulpuntenformule. Je hoeft dus verder met die $-0,5$ niets te doen bij de nulpunten. Je kunt dus vrij makkelijk zien wat de snijpunten met de $x$-as zijn.

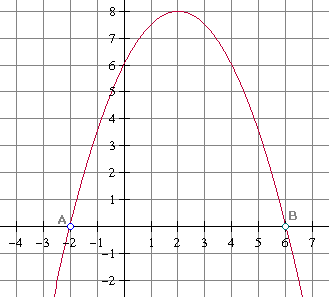
Hopelijk helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 23 november 2014