|
|
|
\require{AMSmath}



Driehoek en omgeschreven cirkel
Gegeven: driehoek ABC, R is de straal van de omgeschreven
cirkel, M het middelpunt van de omgeschreven cirkel en M'
is het midden van MC.
Klopt het dat het midden van AC ligt op de cirkel, met
middelpunt M' en straal R/2, en zo ja hoe bewijst men dat?
Bij voorbaat hartelijk dank !
J.Vrie
Iets anders - woensdag 12 november 2014
Antwoord
Zie de figuur hieronder:
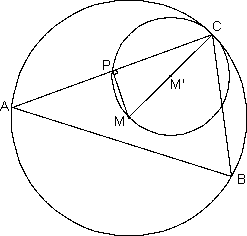
Het snijpunt van AC en de kleine cirkel noem ik P.
MC is een middellijn van de kleine cirkel. Volgens de Stelling van Thales is hoek CPM dan 90°. MP is dus een loodlijn op AC.
Verder: het middelpunt M van de grote cirkel ligt op de middelloodlijn van AC. De loodlijn MP moet dus de middelloodlijn zijn van AC. Het punt P is zodoende het midden van AC.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 13 november 2014
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










