WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Midden lijnstuk

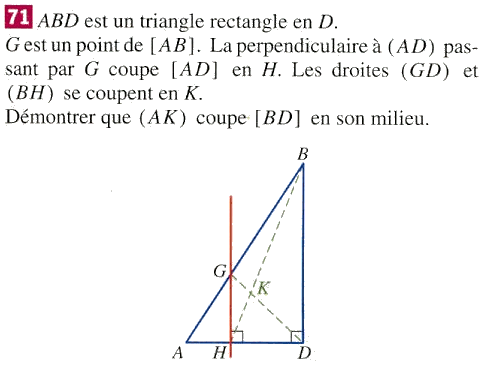In het figuur moeten we bewijzen dat AK, BD in zijn midden snijdt.

G is een willekeurig punt op AB. De loodlijn op AD die door G heen gaat snijdt ad in h. GD en BH snijden elkaar in K.
Yann B
Leerling bovenbouw havo-vwo - zondag 9 februari 2003

Antwoord

Beste Yann,

We zien dat GH en DB parallel zijn, dus de driehoeken KGH en KDB zijn gelijkvormig.

Omdat K in van beide driehoeken het overeenkomende hoekpunt is, is K hun gelijkvormigheidscentrum. Er is derhalve een vast getal t zodat KG/KG = KH/KB = GH/DB = t. Je kunt KGH dus afbeelden op KDB door een rotatie om K van 180°, gevolgd door een bepaalde vergroting van alle afstanden vanuit K.

In het bijzonder wordt het midden van GH hiermee afgebeeld op hetmidden van DB. Dus de verbindingslijn van die middens gaat door K.

De verbindingslijn van de middens gaat ook door A, want driehoek AHG kan op driehoek ADB worden afgebeeld door een vergroting van alle afstanden vanuit A. Het lijnstuk van A naar het midden van HG wordt dan vergroot tot het lijnstuk van A naar hetmidden van DB.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 10 februari 2003