WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Brandpunt en middelloodlijn

F is het brandpunt van een parabool en A is een willekeurig punt van de richtlijn
1. Toon aan dat de middelloodlijn van [AF] een raaklijn is aan de parabool
2. Gebruik deze eigenschap om een raaklijn aan de parabool te construeren die evenwijdig is met een gegeven rechte m.

-$>$ ik heb geprobeerd de vergelijking van de middelloodlijn te bepalen maar dat lukt mij niet
Vandev
3de graad ASO - maandag 12 mei 2014

Antwoord

Hallo Hendrik,

In de figuur hieronder zie je een parabool met brandpunt F, met de richtlijn. Punt A ligt op de richtlijn. Loodrecht boven A vind je punt P op de parabool.

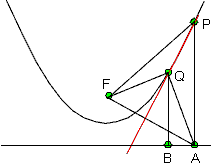
Per definitie geldt: FP = PA

Driehoek FPA is gelijkbenig, dus de rode lijn door P naar het midden van AF is de middelloodlijn van AF.

Stel dat Q een tweede snijpunt van de parabool met deze middelloodlijn zou zijn, het voetpunt van Q op de richtlijn is B. Dan geldt:

FQ = QA (eigenschap van de middelloodlijn FA)

Maar ook moet gelden:
FQ = QB (eigenschap van de parabool)

Dat kan alleen tegelijkertijd waar zijn als punt B en punt A hetzelfde punt zijn. Dan zijn punt P en punt Q ook hetzelfde punt. Er zijn dus geen twee snijpunten P en Q, de parabool en de middelloodpijn van AF hebben slechts één gemeenschappelijk punt. Deze middelloodlijn is dus een raaklijn.

Deze eigenschap kan je gebruiken om een raaklijn n aan de parabool te construeren die evenwijdig is met m, zie de figuur hieronder.

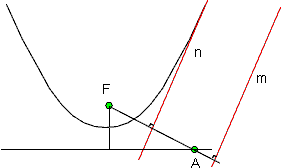
Vanuit F construeer je een loodlijn op m. Het snijpunt van deze loodlijn met de richtlijn is A. De middelloodlijn van AF is evenwijdig aan m en raakt de parabool (zoals we hierboven hebben gezien).

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 12 mei 2014