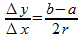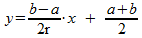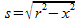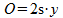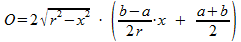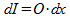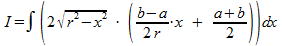WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Volume berekenen van schuin afgesneden cilinder

Beste wisfaq,

De top van een cilinder is aan de bovenkant schuin afgesneden. Het hoogst punt op de top heeft hoogte b en het laagste punt heeft hoogte a. Beide punten liggen boven de basis van de cilinder. De straal van de cirkel is r. Ik wil graag het volume bepalen met behulp van een integraal.

Het volume kan op verschillende manieren worden berekend. Ik moet hier integreren over doorsneden, rechthoekig of trapezoid. Ik moet een uitdrukking A(x) vinden van zo'n doorsnede en dan A(x) integreren van -r tot r.

Om mee te beginnen zie ik niet hoe de doorsnede eruit ziet. Ik begrijp dus niet hoe ik A(x) moet bepalen. Ik heb de hoogte van deze doorsnede nodig en de lengte van de basis van deze doorsnede. Het lukt mij niet op dit te bepalen.

Ik heb begrepen dat de integraal er als volgt uitziet

V=2 INT[√(r²-x²)·((x/2r)(b-a)+¹/₂(a+b))], van -r tot r.

Ik begrijp niet hoe deze integraal is afgeleid.
Het antwoord is ¹/₂·pi·r²(a+b).

Vriendelijke groeten,

Viky

viky
Iets anders - donderdag 10 april 2014

Antwoord

Beste Viky,

In onderstaande figuur zie je de schuin afgesneden cilinder. De getekende doorsnede is een rechthoek.

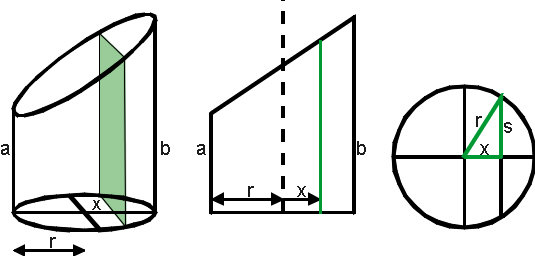
In het middelste plaatje zie je de cilinder recht van de zijkant. De richtingscoëfficiënt van het schuine bovenvlak bereken je met:

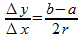
Voor de hoogte y van het bovenvlak geldt zodoende:

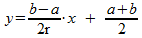
In het rechter plaatje zie je het grondvlak. De halve breedte s van de doorsnede bereken je met:

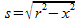
De oppervlakte O van deze doorsnede vind je met:

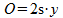
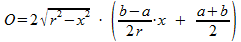
Wanneer we deze doorsnede een dikte dx geven, dan is de inhoud dI hiervan:

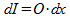
De inhoud van de totale afgesneden cilinder vind je door deze bijdragen dI te integreren voor x=-r tot x=r:

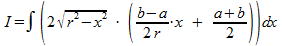
Dit is de integraal die je zoekt.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 10 april 2014