WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Cosinusfunctie omzetten naar sinusfunctie

Hallo
Bij mijn oefeningen in verband met goniometrische functies stond de volgende opgave: Zet het functievoorschrift f(x)=4cos(³/₅x) om naar een voorschrift van de algemene sinusfuncties van de vorm f(x)=a·sin[b(x-c)]. Geef ook de waarde van elke parameter.

Ik snap al dat a=4 blijft en b=3/5 en d=0, maar bij de oplossingen achter in het handboek staat ook dat c=-5$\pi$/6 .

Ik weet ook dat je de cosinus moet omzetten naar de sinus door gebruik te maken van complementaire hoeken, maar als ik dit uitwerk kom ik nooit die c uit. Hoe moet ik dit dan berekenen ?
Maarte
3de graad ASO - zaterdag 29 maart 2014

Antwoord

Als je grafiek van $f(x)=4cos(\frac{3}{5}x)$ plot dan krijg je:

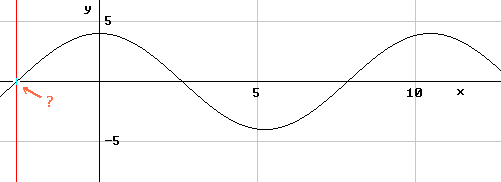
Als je er een 'sinus' van maakt dan verandert de evenwichtstand, de periode en de amplitude niet. Wat wel verandert is de horizontale verplaatsing t.o.v. $O$, de waarde van $c$.

De vraag is dan wat het 'startpunt' is van de functie als sinus. Wat is de x-coördinaat van het punt met het vraagteken?

Dat kan je vinden als je $4cos(\frac{3}{5}x)=0$ oplost, maar dat zal het probleem niet zijn toch?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 30 maart 2014