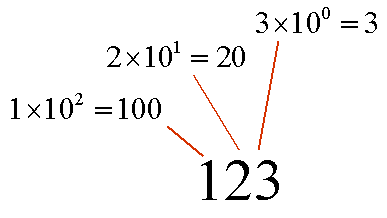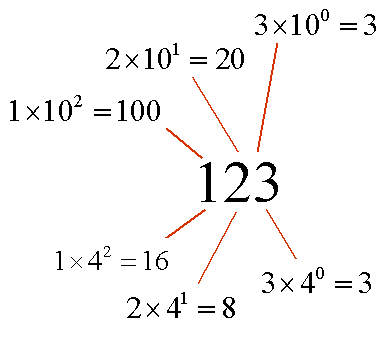WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Viertallig stelsel, tafels en omrekenen

Ik ben bezig om een opdracht voor rekenen wiskunde te maken, waarin ik 4 lessen (groep 8+) moet ontwerpen met een talstelsel. Bij de derde les moet ik de tafels in het viertallig stelsel behandelen en het omrekenen van het viertallig stelsel naar decimaal.

Kan iemand mij vertellen hoe de tafels er uit zien in dit stelsel?

Zelf ben ik bezig dit op te schrijven maar, ik loop vast.
de tafel van 3 in viertallig stelsel:

1x3=3
2x3=12
3x3=21
10x3=30
11x3=33
12x3=102
13x3=111
20x3=120
21x3=123
22x3=132
23x3=201
30x3=211

Kan iemand mij vertellen of ik dit goed doe? In een decimaal stelsel is 20x3 het dubbele van 10x3 namelijk 2x30=60, maar in dit stelsel klopt dit bij 20x3 nog wel namelijk 20x3=60=120 in het viertallig stelsel waarin 40 100 wordt, is 120=2x30 maar bij 30x3 klopt het niet meer want 120+120=300, maar 23x3=201 en 30x3 wordt dan 211.

Kan iemand mij vertellen of ik het op deze manier goed doe?

En hoe werkt het omrekenen van viertallig naar decimaal stelsel? Overal op internet vind ik een uitgebreid verhaal over machtsverheffingen maar ik snap er geen bal van.

mvg,
Jurjen
1e jaars pabo student.
Jurjen
Student hbo - zondag 16 februari 2014

Antwoord

Het tientallig stelsel

De tafel van 3 in het tientallig stelsel?
 1x3 =  3
 2x3 =  6
 3x3 =  9
 4x3 = 12
 5x3 = 15
 6x3 = 18
 7x3 = 21
 8x3 = 24
 9x3 = 27
10x3 = 30
Klaar!

Wij rekenen in het tientallig stelsel. Ons getallenstelsel is een positiesysteem. De waarde van een cijfer hangt af van de positie in het getal. Bij 123 stelt de '3' drie eenheden voor, de '2' stelt twee tientallen voor en de '1' is een hondertal. Elke positie van een getal stelt een macht van 10 voor.

$123=1·10^{2}+2·10^{1}+3·10^{0}$

Met de cijfers 0 t/m 9 kan je allerlei getallen maken, je kunt er mee rekenen, tafels uit je hoofd leren, aftrekken, vermenigvuldigen, delen, machtsverheffen, worteltrekken.. en nog veel meer.

Tellen

Je begint te tellen met 1. Dan komt 2, 3, 4,.. tot 9. Dan ga je over op de tientallen. Die '10' van ons wil dus zeggen '1' tiental en '0' eenheden. Je kunt daarmee doorgaan tot 99. Dan ga je over op de honderdtallen. Onze '100' is dus '1' honderdtal, '0' tientallen en '0' eenheden.

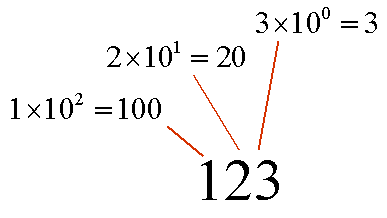
Het viertallig stelsel
Maar hoe zit dat dan in het viertallig stelsel? Hieronder zie je de getallen in het tientallig stelsel (links) met hetzelfde 'aantal' in het viertallig stelsel (rechts):

Bij het viertallig stelsel heb je alleen de cijfers 0, 1, 2 en 3. In het viertallig stelsel schrijf je onze '4' als '10'. In het viertalig stelsel komt '23' overeen met 2×4+3=11 in het tientallig stelsel.

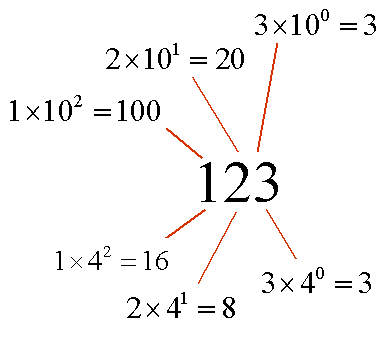
123 is in het viertallig stelsel gelijk aan 1·16+2·4+3=27 in het tientallig stelsel.

De tafel van 3 in het viertallig stelsel
 1x3 =  3
 2x3 = 12
 3x3 = 21
10x3 = 30
...en meer moet het niet zijn.

PS
Ik begrijp niet helemaal wat je nu precies bedoelt met je verhaal over 'dubbel'. Zo is 12 in het viertallig stelsel wel degelijk met dubbele van 3. Er geldt immers 2x3=12, dus daar heb ik geen probleem mee...

Maar je moet nog maar 's kijken, nadenken en verder vragen als je met vragen zit. Liever niet te veel in een keer...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 16 februari 2014