WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Patroon bol van 150 cm doorsnede in 8 stukken maken?

Beste heer mevrouw, ik wil een bol gaan naaien van 150 cm doorsnede (een soort xl strandbal van stof). Ik heb een patroon gemaakt die de oppervlakte van de bol in acht stukken verdeelt. Nu ik hem genaaid heb blijkt hij aan de bovenzijde toch te veel stof (dus oppervlakte) te hebben. Hoe maak ik een juist patroon (1/8 van de oppervlakte van de bol). Ik heb eerste een strandbal in stukken geknipt maar deze is in zes delen verdeeld. Ik wil de bol in 8 delen naaien.

Huidige werkwijze: ik heb een halve cirkel van 150 doorsneden getekend. Op de diameter-lijn heb ik afstanden (in cm) van 5, 10 20 30 enz. geplaatst. Vanaf deze punten heb ik een loodlijn omhoog getekend tot hij de cirkelboog snijdt. Vervolgens een touw op de cirkelboog gelegd en de snijpunten daarop aangebracht.

De afstanden van de diameter-lijn tot het snijpunt met de cirkel is de straal van de segmentcirkel uit de bol, dus bij 5 cm meet ik dan een straal van 27 cm en de berekende omtrek daarbij is dan 170cm. Als ik 8 patroonstukken wil deel ik dit door 8 dus ongeveer 21 cm.

Toen het touw (omtrek halve bol) recht getrokken en op het patroonpapier gelegd en de punten die ik op het touw had aangebracht weer overgebracht op het papier.

Bij het eerste punt hoort de afstand van 21 cm, dus 10,5 aan beide zijden van het rechtgetrokken touw, zo ging ik verder.

Ik realiseer mij dat de bol nooit helemaal een bol kan worden als je heb gaat naaien maar hoe krijg ik hem zo rond mogelijk met 8 stukken?

Ik hoop van harte dat er iemand is die mijn verhaal begrijpt :-) en mij een antwoord kan geven. Bijvoorbaat mijn dank!

Vriendelijke groet
Arjen
Iets anders - zondag 2 februari 2014

Antwoord

Hallo Arjen,

In onderstaande figuur is te zien hoe je de vorm van de stroken kunt bepalen:

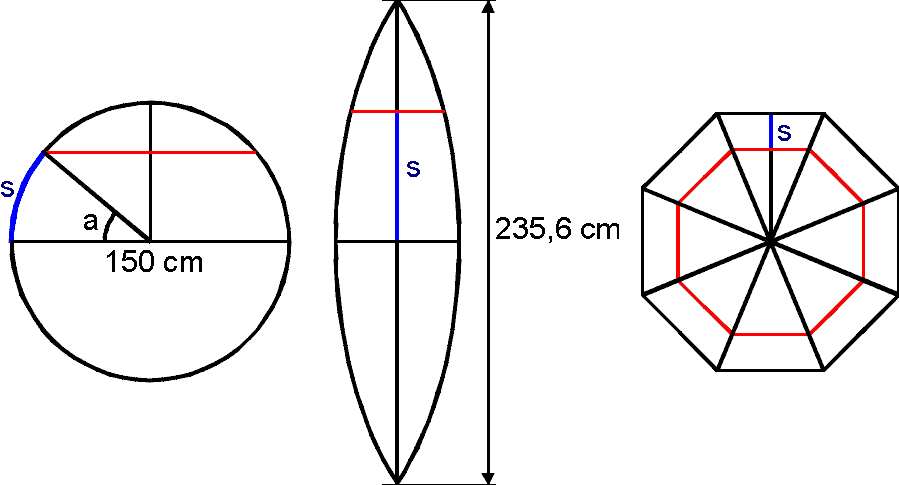
Links zie je het zij-aanzicht van de bol, dan een van de acht stroken (niet op schaal) en rechts het bovenaanzicht.

De omtrek van de bol wordt berekend met:

Omtrek_bol = $\pi$ x diameter = 3,14 x 150 = 471,2 cm

De lengte van elke strook is de helft van de omtrek:

Lengte = ¹/₂ x 471,2 = 235,6 cm

Nu de breedte van de stroken:
Er zijn 8 stroken, de breedte in het midden vinden we door de omtrek te delen door acht:

Breedte_max = ¹/₈x 471,2 = 58,9 cm.

Op een zekere hoogte boven de 'evenaar' heeft de horizontale doorsnede (de rode lijn) dezelfde vorm als het vlak door de 'evenaar', maar alle afmetingen zijn kleiner. We moeten alle afmetingen vermenigvuldigen met de cosinus van hoek a. We vinden de formules:

S = 75 x a (hoek a in radialen).
Breedte_{bij S} = 58,9 x cos(a)

Uitwerken van deze formules geeft voor elke hoogte S boven en onder het midden van elke strook de benodigde breedte, ik heb deze in onderstaande tabel weergegeven.

Het resultaat is een 'strandbal', de rechter figuur geeft het bovenaanzicht. Wiskundig gezien is dit geen bol. De horizontale doorsnedes zijn regelmatige achthoeken. De afstand tussen twee tegenover elkaar liggende hoekpunten is groter dan de afstand tussen twee tegenover elkaar liggende lijnstukken. Dit verschil heb ik gemakshalve verwaarloosd.
Ik verwacht dat, wanneer dit in stof wordt uitgevoerd, de vorm vanzelf nog wat meer bolvormig wordt. Wanneer dit niet goed genoeg is, of waneer je meer wilt weten over de achterliggende berekening, reageer dan gerust op dit antwoord.

S B
0 58,9
5 58,8
10 58,4
15 57,7
20 56,8
25 55,7
30 54,3
35 52,6
40 50,7
45 48,6
50 46,3
55 43,8
60 41,0
65 38,1
70 35,1
75 31,8
80 28,5
85 25,0
90 21,3
95 17,6
100 13,9
105 10,0
110 6,1
115 2,2

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 3 februari 2014

Re: Patroon bol van 150 cm doorsnede in 8 stukken maken?