|
|
|
\require{AMSmath}
Re: Maximum en zadelpunt
Het is wel makkelijker nu, alleen hoe bereken ik zadelpunten, minima of maxima?
Lara R
Student universiteit - maandag 6 januari 2014
Antwoord
Ik neem aan dat zoiets in je boek staat toch?
Kort gezegd gaat dat zo: We hebben 'bedacht' dat als bij een functie van twee variabelen het raakvlak aan de grafiek horizontaal is je mogelijkerwijs (niet noodzakelijkerwijs) te maken zou kunnen hebben met een extreem, dat wil zeggen een maximum of een minimum.
In een punt waar het raakvlak horizontaal is geldt dat de partiële afgeleide naar x en de partiële afgeleide naar y beide nul moeten zijn. Helaas is dat nog geen voldoende garantie voor een maximum of minimum. Het kan ook een zadelpunt zijn. Punten met een horizontaal raakvlak noemen we stationaire punten.
De 'determinant' van Hesse biedt gelukkig een rekenmethode om te bepalen of je bij de gevonden stationaire punten te maken hebt met een zadelpunt of een extreem. Met behulp van de tweede afgeleide naar x en x kan je zelfs bepalen of je bij een extreem te maken hebt met een minimum of een maximum.
Los eerst het stelsel op met de partiele afgeleiden. Dit geeft je de stationaire punten. Vervolgens bepaal je voor die punten fxx, fyy en fxy. Met de determinant van Hesse kan je verder.
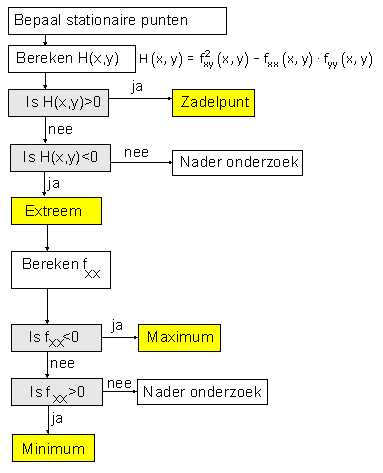
Komt je dat bekend voor?
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 6 januari 2014
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 71864