WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Oppervlakte tussen twee functies en x-as door middel van integreren

Dit is een reactie op vraag 71557

Maar als ik van de functie f(x)=3√x een riemann som wil maken, doe ik dat ook fout. Gegeven is dat de oppervlakte van het gebied gebrensd wordt door de grafiek van f, de x-as en de lijn x=9 en dit oppervlakte wordt bedanderd met een riemann som met 9 deelintervallen. Hoe moet ik hiervan een riemann som maken? Het juiste antwoord is: sigma teken met bovenaan de sigma teken een 8 en onderaan k=0 achter de sigma teken komt: 3√0,5+k. Ik heb nog nooit gewerkt met k=0? altijd met k=1 en daarnaast snap ik niet waarom het 0,5 + k is, wat is die k?

Alvast bedankt
Alex
Leerling bovenbouw havo-vwo - dinsdag 3 december 2013

Antwoord

Hoi Alex,

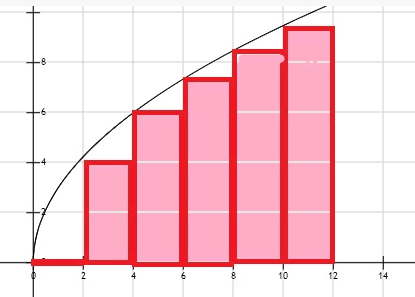
Zie de figuur.

Stel ik wil de oppervlakte weten van de figuur onder de grafiek met als grens.
0-12. Een benadering vind ik goed genoeg dus ik verdeel het in 6 rechthoekjes van gelijke breedte. in dit geval dus van breedte 2. De hoogte van de rechthoek wordt gegeven door de linkerwaarde in de functie te stoppen.

dus 2.f(0)+2.f(2)+2.f(4)+2.f(6)+ 2.f(8)+2.f(10)
Het getal wat ik telkens in de functie stop is 2k beginnende bij 0.
k=0$\rightarrow$0
k=1$\rightarrow$2
k=2$\rightarrow$4
k=3$\rightarrow$6 etc. Ik vervang in de functie dus x met 2k

Dan krijg ik voor de ondersom:
$
\sum\limits_{k = 0}^5 {2.} 3.\sqrt {2k} = 6\sum\limits_{k = 0}^5 {\sqrt {2k} = 6(\sqrt 0 + \sqrt 2 + \sqrt 4 ...\sqrt {10} )}
$

In het geval wat jij beschrijft. Kiest men echter het interval van 0 tot 9 en gebruikt met 9 rechthoeken. De breedte van elke rechthoek is dan dus 1. (9-0)/9=1
Maar ipv de ondersom te nemen of de bovensom kiest men precies het midden van de rechthoekjes om de hoogte te bepalen.

Dus f(0,5)+f(1,5)+f(2,5)....+f(8,5)
Hierbij kiest men dus het midden ( zogenaamde Riemannsom).
Dit schrijf je met een sommatie als volgt:
$
\sum\limits_{k = 0}^8 {3\sqrt {0,5 + k} }
$

DvL

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 3 december 2013