WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Overgangsmatrices

Oefening
Een supermarkt verkoopt twee merken waspoeder, Bright en Shine. Er wordt een derde merk geïntroduceerd, met de naam White. Dit nieuwe merk zou op den duur één van beide andere merken moeten vervangen. De bedrijfsleiding is dan ook erg geïnteresseerd in het koopgedrag van de consument. Er wordt aan 120 klanten die al hun waspoeder kopen bij deze supermarkt gevraagd naar hun koopgedrag. Daarbij blijkt dat ze gemiddeld een maand doen met een groot pak waspoeder van een bepaald merk en dan aan het einde van die maand een nieuw pak aanschaffen. De volgende tabel geeft de wisseling van merken weer:
		Volgende maand	
         		W	S	B	totaal

Deze
maand	W		15	3	2	20
	S		10	25	15	50
	B		15	15	20	50
	totaal		40	43	37	120
Hoeveel van deze klanten hebben in beide maanden waspoeder van het merk Shine gekocht?
Hoeveel procent van de klanten is van merk gewisseld?
Stel voor de overgangen van het éne merk naar het andere een graaf en een overgangsmatrix W op.
Welke overgangsperiode kent de graaf?
De bedrijfsleiding gaat ervan uit dat deze overgangen voor de komende maanden blijven gelden.
Stel je nu voor dat aanvankelijk de verdeling voor de merken Bright en Shine als volgt was: 35% van de klanten koopt Bright en 65% van de klanten koopt Shine. Bereken dan de verdeling van de klanten over de drie verschillende merken na de introductie van het merk White.
Ik heb een vraag bij c en e
Bij c moet deze in% gegeven worden? Dan heb ik
             van
       0,125     1/12    0,125
naar     0,025    5/24   0,125
        1/60     0,125     1/6
Is het antwoord op e de kolommatrix met de getallen 0,78, 24? En dan zou ik na 1 maand hebben 11,75 en 21,5 en 16,75?

Alvast bedankt
Dina
3de graad ASO - maandag 2 december 2013

Antwoord

Ik heb alleen even naar oefening 1 gekeken. Bij oefening 2 zie ik ook geen graaf, dus daarover moet je dan maar even een nieuwe vraag stellen. Dat is sowieso handiger... Eén vraag per vraag...

Bij oefening 1 krijg ik bij c. zoiets als:

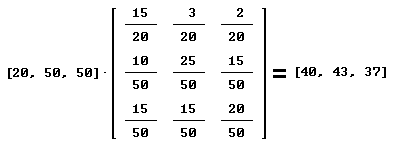
...en bij e. krijg ik dan:

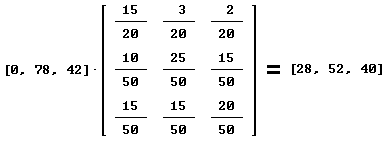
Dat is dan ongeveer, afgerond dus. Die 42 komt van 35% van 120 en die 78 van 65% van 120.

Ik heb alleen de 'van' en 'naar' verwisseld...

Dat maakt verder niet uit, behalve dan dat je vermenigvuldiging omgedraaid is. Je kunt ook de matrix even spiegelen en dan vermenigvuligen met de kolommatrix. Die komt dan wel achter de matrix en niet ervoor...

Hopelijk heb je er iets aan.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 2 december 2013

Re: Overgangsmatrices