WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

2 maal 45 graden

Als ik een vlak onder 45 graden plaats en ik wil daar haaks, dus onder 90 graden, een ander vlak op laten aansluiten dat ook onder 45 graden staat, welke hoek maakt dan het snijvlak?
hiske
Student hbo - donderdag 7 november 2013

Antwoord

Hallo Hiske,

Als ik je vraag goed begrijp, is dit de situatie:

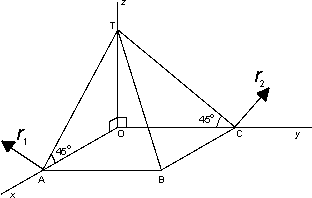
De lijnstukken AB en BC staan loodrecht op elkaar, de vlakken ABT en BCT staan onder een hoek van 45 graden met het grondvlak OABC. De vraag is dan: wat is de hoek tussen de vlakken ABT en BCT?

Je kunt dan kijken wat de hoek is tussen twee vectoren r₁ en r₂ loodrecht op deze twee vlakken. Ik heb gekozen voor vectoren met de richting r₁ = (1, 0, 1) en r₂ = (0, 1, 1). We berekenen het inwendig product van deze vectoren:

r₁.r₂ = x₁x₂ + y₁y₂ + z₁z₂
r₁.r₂ = 1×0 + 0×1 + 1×1 = 1

Ook geldt:
r₁.r₂ = |r₁|×|r₂|×cos($\alpha$)
Hierin is |r₁| de lengte van r₁, |r₂| de lengte van r₂ en $\alpha$ is de hoek tussen de vectoren.

De lengte van r₁ en r₂ berekenen we met Pythagoras:
r₁ = √2
r₂ = √2

Dus:
√2×√2×cos($\alpha$)=1
cos($\alpha$)=¹/₂
$\alpha$=60°

Nu vertalen we dit naar de hoek tussen de vlakken. De hoek $\alpha$ is de 'knik' die de vlakken maken, zie onderstaande figuur:

Wellicht ben je meer geïnteresseerd in de hoek aan de binnenkant van de piramide, deze is dan 180-60=120°.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 8 november 2013