WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Doelschop gemist !

Dag wisfaq,
Bij een voetbalwedstrijd wordt , rakelings langs de grond, een doelschot afgevuurd van op een hoek van de grote backlijn(afmetingen 40.32 m en 16.5 m. De bal mist doel en overschrijdt de achterlijn op 1 meter van het doel(afmetingen 7.32m op 2.44m) Hoe groot is de kleinste afstand tussen bal en doel tijdens het traject van het(gemiste) doelschot.
Neem ik de afstand tussen de buitenkant doel en het eindpunt van de grote backlijn, dan vind ik 40.32-7.32/2 =16.5 m. Als de bal het doel van rechts naar links voorbij zoeft en op een meter buiten de paal de achterlijn overschrijdt dan moet daar " ergens" het kortste punt liggen (zou 0,55m moeten zijn).
Een goede tekening en een aanzet van hoe ik moet voortwerken zou al wel wat duidelijkheid geven, denk ik..
groetjes en dank jullie voor de tijd .
Rik
Rik Le
Iets anders - woensdag 2 oktober 2013

Antwoord

Als ik het goed begrijp, is dit de situatie (schets niet op schaal):

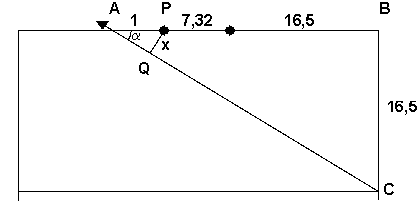
De bal wordt weggeschoten in punt C en passeert de doellijn in punt A, 1 meter naast de doelpaal P. De kortste afstand tussen de bal en het doel is de afstand tussen P en Q, deze noem ik x.

In de rechthoekige driehoek ABC kunnen we de hoek a berekenen:

tan(a)= ^16,5/_{(16,5 + 7,32 + 1)}.

Wanneer a bekend is, berekenen we x in de rechthoekige driehoek APQ:

x = 1×sina

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 oktober 2013