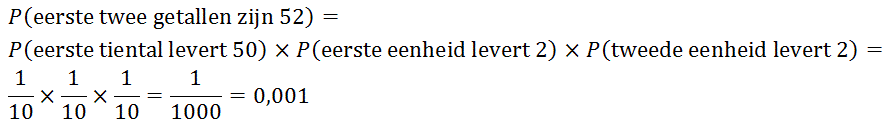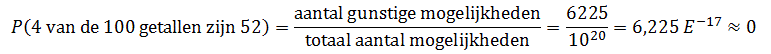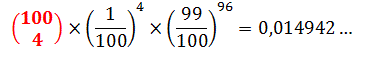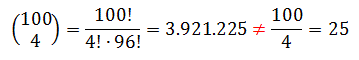WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Verschillende modellen voor een trekking 2 uit 100

Dit is een reactie op vraag 70659

Beste Thijs,
Dank voor je uitgebreide antwoord. Het is me nu duidelijk dat methode 1 afwijkt. Methode 3 heb ik onduidelijk uitgelegd, ik doe namelijk 20 trekkingen en geen 100.
Als de in de eerste trekking van 10 ballen een 5 wordt getrokken dan geldt dat getallen in de hele RIJ van de matrix een 5 als 10-tal waarde hebben. Vervolgens trek ik de Y-waarden. Als 2 valt dan krijg ik dus 52 in de rij van 5. Als daarna wéér 2 getrokken wordt (een kans van 1/10) dan heb ik dus 2x 52 achter elkaar. Elke keer is de kans 1/10 dat twee opeenvolgende getallen hetzelfde zijn 'ín dezelfde rij of kolom'. Bij methode twee doe ik 100 trekkingen, bij methode 1 slechts 20, en niet 100, zoals je aangeeft. Dat geeft mij een intuïtief gevoel van kansverschil. Maar is de kans op bijvoorbeeld 4x 52 wél gelijk bij methode 2 en 3? Tenslotte krijg ik een andere uitkomst uit de berekening: 100/4 x (1/100)^4 x (99/100)^96 = 25 x 0,00000001 x (0,99)^96 = 0,000000095. Of doe ik iets niet goed?
Erwin
Iets anders - woensdag 24 juli 2013

Antwoord

Dag Erwin,

Oke, dan heb ik methode 3 inderdaad verkeerd begrepen. Als ik een simulatie van methode 3 zou maken in excel, zou dat er dan als volgt uit komen te zien ongeveer?

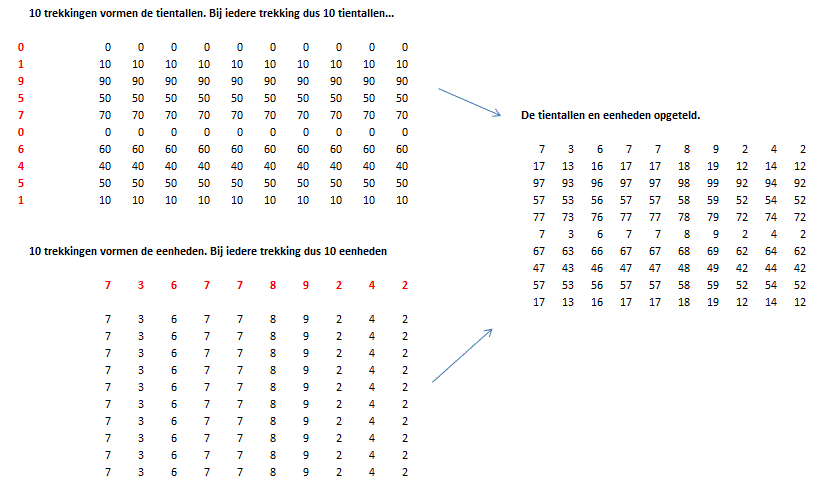
Dan is de situatie inderdaad anders, en inderdaad niet gelijk aan methode 1 of 2. Maar de vraag is nu dan of de willekeurigheid nog eerlijk is. 1 trekking levert namelijk voor 10 van de 100 getallen al een behoorlijke beperking op. 1 trekking van een tiental, zorgt ervoor dat er 10 getallen zijn die nog maar 10 opties kunnen hebben. Dat is niet meer echt willekeurig.

Maar dan had je gelijk..

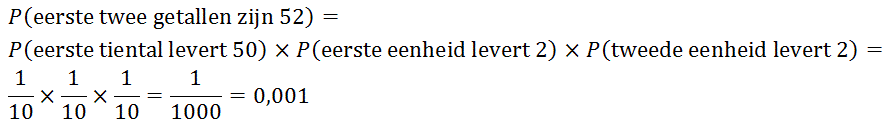
Die kans is dus veel groter. Omdat bij de eerste trekking, al vastligt dat de eerste 10 getallen (dus ook de eerste 2) het zelfde tiental hebben. De willekeurigheid is dus behoorlijk beperkt.

De vraag hoe groot de kans is dat van 100 getallen, er vier 52's tussen zitten, is een iets lastigere vraag. De eerste vraag is hoeveel combinaties dat er zijn, zodat er vier 52's ontstaan. Dat kan op 3 verschillende manieren:

- 4 tientallen van 50 + 1 eenheid van 2
- 2 tientallen van 50 + 2 eenheden van 2
- 1 tiental van 50 + 4 eenheden van 2

De volgende vraag is: Hoeveel permutaties (rangschikkingen) zijn er per combinatie mogelijk?

Dus er zijn 2100 + 2025 + 2100 = 6225 gunstige mogelijkheden (mogelijkheden om 4 van de 100 getallen, 52 te laten zijn).

In totaal zijn er 10²⁰ mogelijkheden om getallen te maken (want iedere bal die je trekt, heeft 10 mogelijkheden).

De kans dus dat er 4 van de 100 getallen, 52 zijn, is gelijk aan:

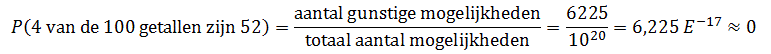
Die kans is dus nihil.

Tenslotte die laatste berekening waar jij het over hebt. Ik bereken:

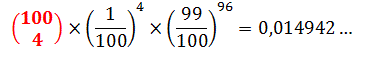
Die rode factor is niet 100/4=25. Maar die rode factor geeft aan op hoeveel manieren die 4 keer 52 getrokken kan worden.
Die 52 kan namelijk meteen op het begin 4 keer gekozen worden. Maar ook de 1e, 2e, 3e en 5e keer. Of 1e, 3e, 27e, 83e keer. Dat kan dan op '4 uit 100' verschillende manieren. Of ook wel '100 boven 4' manieren. Die '100 boven 4' komt overeen met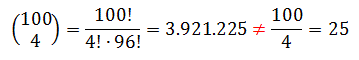

In ieder geval: De beste willekeurigheid zit in methode 2. En de 3 methodes zijn dus zeker niet gelijk aan elkaar.

Ja het is me wat, behoorlijk wat info. Kom je er nog uit?

Succes ermee..

Groet

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 24 juli 2013