WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte cirkel in vierkant

'Bewijs dat de oppervlakte van de cirkel omgeschreven aan een vierkant het dubbel is van de oppervlakte van de cirkel, ingeschreven in dit vierkant.'

Bij deze opgave zat ook een tekening van een cirkel met daarin een vierkant en in dat vierkant nog een cirkel (er staan geen andere gegevens bij). Je moet dus bewijzen dat de oppervlakte van de grote cirkel, het dubbele is van de oppervlakte van de kleine cirkel. Aangezien dit zich in het hoofdstuk 'driehoeksmeting in rechthoekige driehoeken' bevindt, heb ik in de vierkant al een diagonaal getekend zodat je 2 rechthoekige driehoeken hebt. De diagonaal is gelijk aan de diameter van de buitenste cirkel en de zijde van het vierkant is de diameter van de kleine cirkel.

Ik heb al wat zitten puzzelen met sin, cos en tan maar kan het maar niet vinden... Alvast bedankt!
lotte
2de graad ASO - zaterdag 15 juni 2013

Antwoord

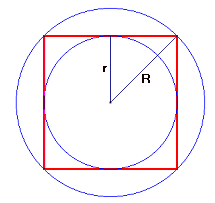
Oppervlakte omgeschreven cirkel: $\pi$R²
Oppervlakte ingeschreven cirkel: $\pi$r²

R=√(r²+r²)=r√2

..en dan ben je er al bijna...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 15 juni 2013