WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Voorwaardelijke kansen

Beste allemaal,

Voor mij ligt de volgende opgave:
Er wordt een proefwerk A en B afgelegd. Voor proefwerk A heeft 70 % een voldoende. Van de leerlingen die voor proefwerk A een voldoende hebben heeft 60 % een voldoende voor proefwerk B. Van die leerlingen die proefwerk A niet haalde heeft 50 % een onvoldoende voor proefwerk B.

Vraag 1.
Bereken de kans dat een willekeurige leerling voor proefwerk B een voldoende haalt.

Ik dacht dan P(onvoldoende A voldoende B)+ (P voldoende A voldoende B) dus (0,3 x 0,5) + (0,7 x 0,6) = 0,57
Is dit correct?

Vraag 2.
Hoe groot is de kans dat een leerling een voldoende voor proefwerk A heeft als bekend is dat hij voor proefwerk B een voldoende heeft.

Ik dacht: P = 42 / 15 + 42 = 0,7368

Vraag 3 (waar ik niet uitkom).
Gebeurtenis A: Voor proefwerk A voldoende
Gebeurtenis S: Voor proefwerk B voldoende

Onderzoek (met een berekening) of deze gebeurtenissen onafhankelijk zijn.

P (A) = 0,7
P (A/S) = 42 / 57 = 0,74

Dus zijn ze afhankelijk. Klopt dit?

Graag hulp

Gr,

Joep
Joep
Leerling bovenbouw havo-vwo - woensdag 8 mei 2013

Antwoord

Helemaal in orde. Ik vind zelf een kanstabel altijd erg handig:

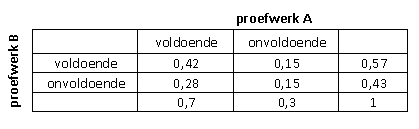
Bij c. is het gebruikelijk om te laten zien dat bij onafhankelijkheid geldt:

P(A en S)=P(A)·P(S)

In dit geval zou 0,7·0,57 gelijk moet zijn aan 0,42. Dat is niet het geval dus niet onafhankelijk.

Zie ook 5. (On)afhankelijkheid

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 8 mei 2013