WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Halveren van 2 cirkels door een derde cirkel

Vraag: Zoek de meetkundige plaats van de punten, die 2 gegeven cirkels C(M,r1) resp. C(N,r2) halveren.

Bemerking: Triviaal zou zijn om te kiezen voor de rechte die beide middelpunten van de 2 cirkels gaat verbinden.
Op zicht is dit zelfs onmiddellijk duidelijk.
Ik vermoed dat deze meetkundige plaats wellicht ook een cirkel kan zijn. Bij het lezen van de opgave dacht ik meteen aan de volgende stelling: "Elk punt van de machtlijn van 2 gegeven cirkels, dat binnen of op de cirkels ligt, is het middelpunt van een cirkel, die door de 2 gegeven cirkels wordt gehalveerd."

Ik heb echter het gevoel dat ik die stelling niet kan gebruiken om tot een oplossing te komen van het vraagstuk, want dan zou elk van de gegeven cirkels moeten gekoppeld kunnen worden aan 2 andere cirkels, waarvan de machtlijnen resp. M en N bevatten. Dit lijkt mij niet zinvol om hier verder te zoeken!

Verdere denkpistes: (1) De gezochte meetkundige plaats (cirkel) moet door de eindpunten van een middellijn gaan, zowel bij C(M,r1) als bij C(N,r2) (betekenis van halveren!). Noem deze middellijnen AB resp. CD. Dan betekent dit dat de punten A, B, C en D een koordenvierkhoek moeten vormen van de gezochte cirkel, die overeenkomt met de gezochte meetkundige plaats. Twee zijden zijn gekend, nl AB=2.r1 en CD = 2.r2. Daar de juiste stand van deze middellijnen niet a priori is gekend, is het onmogelijk in te schatten, hoe groot de zijden BC en AD zijn. Bovendien geldt dat ook voor de diagonalen van die koordenvierhoek. M.a.w. de stelling van Ptolemaeus zal hier ook niet veel helpen.

(2)Veronderstel dan dat P het middelpunt zou zijn van de gevraagde cirkel, dan geldt in DMNP als MP>NP:
MP²-NP²=MN . QP' resp. NP²-MP²=NP'.QP' als MP < NP
Met Q het midden van MN en P' de projectie van P op MN.
Daar je niets weet over de grootterelatie van MP en NP, is het onmogelijk om te weten of je nu P' links van Q of rechts van Q moet aanduiden. Bovendien geeft dat ook geen enkele informatie aangaande de juiste ligging van het middelpunt P van de gevraagde cirkel.

Vraag: Graag had ik een tip of enige tips gekregen om dit probleem te kunnen oplossen.

Opmerking: De omgekeerde weg is natuurlijk makkelijker... je kan eerst de gevraagde cirkel tekenen, vervolgens hier 2 koorden AB en CD aanbrengen. En op elke koorde teken je een cirkel met middellijn AB resp. CD.
Dit doet mij in elk geval vermoeden dat het omgekeerde van dit omgekeerde ook moet mogelijk zijn.
Bedankt voor de hulp!
Yves D
Docent - woensdag 6 februari 2013

Antwoord

Dag Yves,
Met de wellicht wat eigenaardige definitie van het halveren van een cirkel is de constructie of bepaling van de meetkundige plaats van de middelpunten van de cirkels die de twee gegeven cirkels "halveren" een stuk eenvoudiger dan echt halveren.
Als ik het goed begrijp is het probleem dus:
Gegeven: Twee cirkels (M₁,r₁) en (M₂,r₂) met afstand tussen M₁ en M₂=d.
De middellijnen van deze cirkels zijn koorden van een derde cirkel(P,r₃).
We zoeken de meetkundige plaats van P.

Je gaf al aan dat de ontaarde cirkel, met straal oneindig een oplossing is.

Met een analytische aanpak kom je al snel tot de oplossing:
Kies de x-as langs de as, de lijn door M₁ en M₂. Kies de oorsprong midden tussen M₁ en M₂. Kies een willekeurig punt P(x,y).
Trek PM₁ en PM₂. Trek ook de middellijnen hier loodrecht op. (zie tekening: AB en CD. )
Nu moet gelden dat PA=PC. Dus (x+d/2)²+y²+r₁²=(x-d/2)²+y²+r₂².
En dan blijkt x onafhankelijk van y, dus de meetkundige plaats van P is een lijn loodrecht op de as.
We kunnen dat construeren door het punt P op de x-as te bepalen.
Daarvoor gebruik je de koordenvierhoek EFGH (=gelijkbenig trapezium) (Zie tekening).

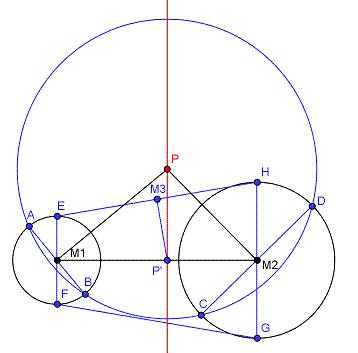
Het is een leuk vraagstuk en ik hoop hiermee de eenvoudigste oplossing te hebben gesuggereerd.
Lieke.

ldr

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 10 februari 2013