WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Differienteren en zo...

vraag 1: De begindruk in een vat bedraagt 2 bar. Deze druk stijgt 10% per sec
A) bereken de druk nar 3 sec
B) bereken de drukverschil na 3 sec

vraag 2: Bepaal de raaklijn aan de funktie f(X) = 3* in * = 2
Df = (1,3)

vraag 3: F(x)= 4 cos x + 1 Df= (0,2pie)
Bepaal het bereik Bf, schets de garfiek en bepaal de raaklijn x = 0,75pie

Vraag 4: Eeen persmachine werkt volgens h(x)= 60 sin (pie t) cm met t in sec Wat is de periodetijd en bereken de perssnelheid na 1,25 sec

Vraag 5: F(x) = h(x) * g(x) * = maal

h(x) = x tot de macht 3 g(x) = 2e* * = x

Bepaal de afgeleide van F(x) als x=4

richar
Leerling mbo - zaterdag 18 januari 2003

Antwoord

Beste Richard,

Vraag 1
Je weet dat 10% = 0,1 en dat de begindruk (dus bij 0 sec) 2 bar bedraagt. De druk stijgt per seconde met 10% dus is er een exponentiële groei. Je kunt met deze gegevens een exponentiële functie opstellen, want beginfactor is 2 en de groeifactor is 1,1 (want er is een toename van 10% m.a.w. het oorspronkelijke getal vermenigvuldigen met 1,1 want het oorspronkelijke getal (= ´1) neemt met 0,1 toe (= 0,1 + 1 = 1,1)).
Þ p(t) = 2 ´ 1,1^t waarin p = druk, t = tijdseenheid in seconde.

De druk na 3 seconden is p(3) = 2 ´ 1,1³ = 2,662 bar. Je zou ook de druktoenamevan de eerste seconde kunnen berekenen 2´0,1 = 0,2 bar dus in totaal na één seconde 2 bar + 0,2 bar = 2,2 bar. Na de 2^de seconde komt hiervan weer 10% bij, dus (2,2)´0,1 = 0,22 bar, maar in totaal was er al 2,2 bar dus 2,42 bar en voor de 3^de seconde hier weer hetzelfde voor toepassen, maar met de functie gaat het veel sneller (wel natuurlijk een goed hulpmiddel om de functie op juistheid te controleren).

B) Hier wordt hoogstwaarschijnlijk het drukverschil t.o.v. het begin bedoeld. f(3) - f(0) = 2,662 - 2 = 0,662 bar.

Vraag 2
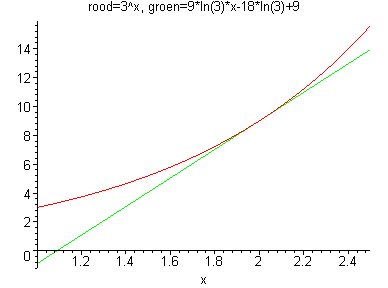
Je bedoelt f(x) = 3^x en hiervan de raaklijn in het punt x = 2? Algemeen kun je met deze formule de raaklijn aan een grafiek opstellen
y - y_waarde = f'(x)´(x - x_waarde)
Eerst de y-waarde bepalen f(2) = 9 en de afgeleide van f(x) = 3^xln(3), dus f'(2) = 9´ln(3).
y = 9 ln(3)´(x - 2) + 9
y = (9 ln(3))x - (18 ln(3)) + 9

Vraag 3
Het bereik wil zeggen : welke y-waardes kan de functie aannemen? Algemeen is bekend dat de cosinusfunctie gedefinieerd is tussen y = -1 en y = 1. Hier neemt de cosinus dus minimaal -1 in, krijg je 4´(-1) + 1 = -3 en maximaal kan de cosinus 1 worden, dus 4 + 1 = 5 dus de grafiek heeft als bereik [-3, 5].

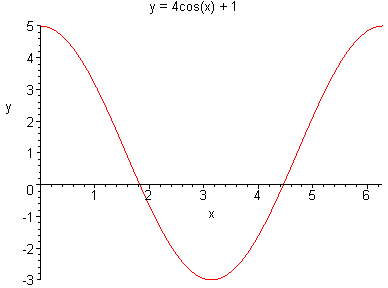
Wat de raaklijn betreft, dat gaat via dezelfde manier als de vorige opdracht. Ik zal je op weg helpen met de afgeleide (4 cos(x) + 1)' Û (4 cos(x))' + 1' Û 4´(cos(x))' + 0 (want de afgeleide van een constante is 0). (cos(x))' = -sin(x) Þ (4 cos(x) + 1)' = -4 sin(x).
Nu kun je zelf verder?

Vraag 4
Je moet je bij deze vraag niks aantrekken van de 60 wat de periode betreft, want die geeft gewoon aan dat de y-waardes vermenigvuldigd wordt met 60 (m.a.w. de amplitude is 60).
De periode van sin(ax) = 2p/a Þ hier toegepast 2p/p = 2. Je zou dit ook via de grafische methode opgelost kunnen hebben, want je weet dat het bereik van de functie het interval [-60,60] is, dus je zou de functie kunnen plotten van zeg x Î [0,p] en y Î [-60,60] je weet dat de periode inhoudt dat er precies één golfbeweging is die een gelijke uitslag boven als onder de x-as heeft. Je kunt afleiden dat dit geldt voor x = 0 tot en met x = 2, dus de periode is 2.

Dan de perssnelheid. De snelheid kun je berekenen door de afgelegde weg (dus hoeveel cm er geperst wordt) te differentiëren. Dus (60 sin(pt))' = 60 (sin(pt))'
Nu moet je weten dat (sin(x))' = cos(x), en je moet gebruik maken van de kettingregel. Stel u = pt Þ du/dt = p; y = sin(u) Þ dy/du = cos(u) = cos(pt)
Þ du/dt ´ dy/du = pcos(pt).
Maar het was 60 (sin(pt))' Þ 60pcos(pt). Je wilde de snelheid weten op het tijdstip t = 1,25 s dus 60pcos(1,25p) = -133,2864880 cm/s in km/h is dat omgerekend -4,788 km/h het is dus een negatieve snelheid, m.a.w. de pers komt dan terug naar boven (opwaartse kracht door geperste materiaal) en is dus negatief.

Vraag 5
Let op met hoofdletters! Indien je begint met integreren ga je primitiveren (da's het omgekeerde differentiëren) en voor de primitieve gebruik je hoofdletters. Bij deze opgave wil je het product h(x)g(x) toekennen aan F(x). F(x) = x³´2e^x
Þ F(x) = 2x³e^x.
F'(x) = 2(x³e^x)'. Hier moet je gebruik maken van de productregel die zegt (f´g)' = f'g + g'f. Hier toegepast F'(x) = 2( (x³)'(e^x) + ( (e^x)'(x³)))
Û F'(x) = 2(3x²e^x + e^xx³) Þ F'(x) = 2(x²e^x(3 + x)) Þ F'(x) = 2x²e^x(3 + x) en dit zou je eventueel nog kunnen uitschrijven in 6x²e^x + 2x³e^x.

Dus F'(4) = 8e^x(12 + 16) Þ F'(4) = 224e⁴ oftewel 12229,98561...

Een heel verhaal, maar hopelijk is het duidelijk.
Indien je iets niet begrijpt, stel gerust nog een vraag.

Groetjes,

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 19 januari 2003