WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Formule maken bij een kwadratisch verband

Ik heb deze tabel:

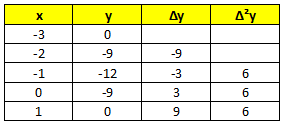
Nu moet ik uit deze tabel een kwadratische formule halen die 3x²+6x-9 moet luiden volgens het antwoordenboekje. Ik weet hoe ik aan 3x² moet komen, want dat is gewoon y:2 (6:2), maar hoe ik aan de rest van de formule kom?

Asjeblieft help mij, want ik heb morgen tentamens...
Martin
Leerling bovenbouw havo-vwo - donderdag 16 januari 2003

Antwoord

Er zijn verschillende manieren om dit probleem aan te pakken, zie Kwadratische formules en parabolen voor voorbeelden en achtergronden.

Omdat de tweede verandering constant is weet je dat het verband kwadratisch is. De algemene formule voor een kwadratisch verband is:

y=ax²+bx+c [1]

De kunst is nu om de waarden van a, b en c te vinden. We zien dat (0,-9) een punt is van de parabool. Invullen in [1] levert c=-9.

Neem nu de punten (-3,0) en (-2,-9). Invullen levert:

a·(-3)²+b·-3-9=0
a·(-2)²+b·-2-9=-9

9a-3b=9
4a-2b=0

18a-6b=18
12a-6b=0
--------- -
6a=18
a=3
b=6

De formule wordt: y=3x²+6x-9

Deze methode werkt altijd, maar in dit geval kan het sneller. Je weet immers de nulpunten: (-3,0) en (1,0). Dus y=a·(x+3)(x-1) is ook een goede formule voor de parabool. Vul nog een punt in om a uit te rekenen, bijvoorbeeld (0,-9):
-9=a·(0+3)(0-1)=a·-3
a=3
Enz...

Overgens als je een TI83 gebruikt kan je nog iets grappigs doen. Er zit namelijk een functie op je GR om de coëfficiëenten van tweede-, derde- en zelfs vierdegraads functies bepalen. Zie opstellen derdegraads functie bij vier punten voor een voorbeeld of kijk in je handleiding.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 16 januari 2003