|
|
|
\require{AMSmath}



Hoek berekenen
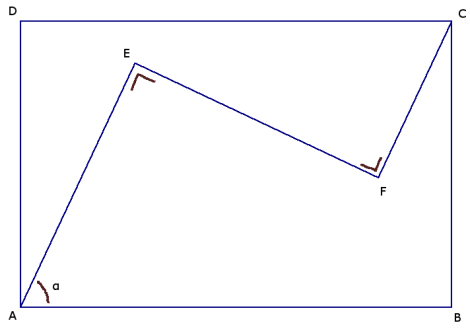
Het betreft een rechthoek ABCD, waarvan A en C zijn verbonden via E en F, waarbij AEF en EFC rechte hoeken zijn.
Gegeven zijn: AB, AD, AE en CF.
Gevraagd is hoek $\alpha$.
Met mijn poging tot oplossen ben ik gekomen tot de volgende vergelijking:
tan(á)=AB-(AEcos(á)+CFcos(á))/AD-(AEsin(á)+CFsin(á))
Is deze vergelijking al op te lossen? Of ontbreekt er nog wat? Of zit ik misschien helemaal in de verkeerde richting te denken?
Wouter
Iets anders - vrijdag 21 oktober 2011
Antwoord
Dag Wouter,
Ik heb niet geprobeerd jouw uitdrukking te controleren.
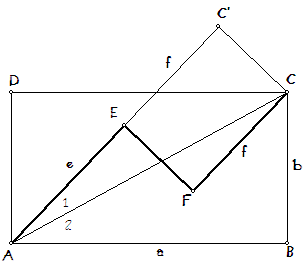
Ik heb het punt C (als C') op de lijn AE loodrecht geprojecteerd.
Met de lijn AC wordt de gezochte hoek dan in twee stukken verdeeld.
Van het ene deel (in het plaatje aangegeven met 1) kan je via de cosinus de grootte berekenen. Immers e en f zijn bekend, dus ook AC' = e + f, en via a en b is ook de lengte c van AC bekend (Pythagoras).
En van het andere deel (aangegeven met 2) is de grootte via de tangens te berekenen.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 22 oktober 2011
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











