|
|
|
\require{AMSmath}



Combinaties
Helaas lukt het mij niet de nu volgende uitwerking te doorgronden. Voor jullie waarschijnlijk erg simpel, maar voor mij "zeker" volkomen duister. x boven 2 = 105 impliceert:
x!/2!(x-2)!=105
1x2x3x..x(x-3)x(x-2)x(x-1)x iks/(1x2)x1x2x3x...x(x-3)x(x-2)
=105 (nu gelijke factoren in de teller en noemer wegdelen)
 (x-1)x/2=105 (x-1)x/2=105 x2-x-210 = 0 ,x=-14 of x=15.Niks aan de hand,alles duidelijk.Maar hoe zit het dan met x boven 3 = 35.Ik kom er niet uit. x boven 3=35 x2-x-210 = 0 ,x=-14 of x=15.Niks aan de hand,alles duidelijk.Maar hoe zit het dan met x boven 3 = 35.Ik kom er niet uit. x boven 3=35 x!/4!(x-4)!=35 x!/4!(x-4)!=35
 (x-1)x/4=35 (x-1)x/4=35 x2-x-140=0.En nu lig ik eraf.Er moet 7 uikomen,dat weet ik . x2-x-140=0.En nu lig ik eraf.Er moet 7 uikomen,dat weet ik .
Alvast hartelijk dank.
P.S.Mischien wat laat maar bedank JR alsnog voor zijn razendsnelle antwoord op mijn vraag van 22-12-2002.
kees
Leerling bovenbouw havo-vwo - zaterdag 11 januari 2003
Antwoord
Is het niet zoiets?
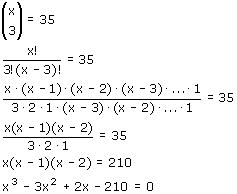
Even oplossen  en je ziet: en je ziet:
x=7Wel een beetje overdreven... Je weet x is een geheel getal, groter dan 3... 4?, 5?, 6? 7? Ja! Gaat misschien wel net zo snel! Als je een grafische rekenmachine kan het nog sneller..., maar ja dat is dan weer een heel ander verhaal!

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 11 januari 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 (x-1)x/2=105
(x-1)x/2=105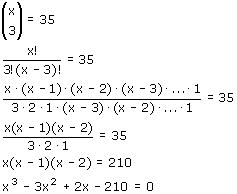
 en je ziet:
en je ziet: 
