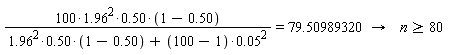|
|
|
\require{AMSmath}



Percentage respondenten populatieonderzoek
Binnen mijn onderzoek heb ik tevredenheid onderzocht via interviews onder alle mensen van een bepaalde organisatie (dat zijn er ongeveer 100). Nu heb ik gelezen dat dit een populatieonderzoek heet. Voor de verantwoording van het onderzoek ben ik op zoek naar het percentage voor een betrouwbare uitkomst wat betreft het aantal respondenten. In totaal heb ik 40 mensen middels een interview gesproken (= 40%). Kunt u mij vertellen of er een percentage voor betrouwbaarheid bij dit soort onderzoeken bestaat en wat het percentage zou kunnen zijn?
Alvast bedankt!
Sophie
Student hbo - zondag 1 mei 2011
Antwoord
Dag Sophie,
Ik heb even wat huiswerk gedaan op internet en ben bij de volgende site uitgekomen: www.marktonderzoek.punt.nl . Hierop staat een formule om een steekproefgrootte (aantal respondenten) te berekenen bij bepaalde gegeven factoren:
De formule voor een steekproef waarbij de populatie eindig is:
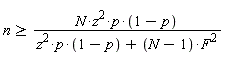
Hierbij is:
n = het aantal benodigde respondenten. Altijd naar boven afronden
z = de standaardafwijking bij een bepaald betrouwbaarheidspercentage. Dus 1,96 bij 95% betrouwbaarheid. Deze wordt bijna altijd gebruikt. Dit betrouwbaarheidspercentage (en daarmee de standaardafwijking) moet je zelf bepalen. Dit percentage wil bijvoorbeeld zeggen: Stel je neemt de enquete 100 keer achter elkaar af (en je deelnemers hebben een korte termijn geheugen ofzo, dat ze steeds vergeten wat ze de eerdere keer ingevuld hebben). Dan moet er in 95 van de 100 gevallen de zelfde resultaten uit komen rollen (een enquete is immers een momentopname).
N = de grootte van de populatie
p = de kans dat iemand een bepaald antwoord geeft (in de meeste gevallen 50%) -- tevreden, ja of nee... Om safe te spelen stel je dat de beide uitkomsten even veel kans hebben. tevreden, ja of nee... Om safe te spelen stel je dat de beide uitkomsten even veel kans hebben.
F = de foutmarge vaak wordt hierbij 3%, 5% of 7%. Ofwel nauwkeurigheidsafwijking: Als uit je steekproef volgt dat 70% tevreden is, dan kan het in werkelijkheid tussen de 65 en 75 procent liggen (als je voor foutmarge van 5% kiest). In de meeste gevallen wordt gekozen voor 5%.
De (gewenste) gegevens invullen in de formule levert een minimale steekproefgrootte op (minimum aantal respondenten):
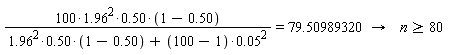
Je komt dus nog 40 mensen te kort, als je aan een betrouwbaarheid van 95 procent wilt voldoen en een foutmarge van 5 procent.
Je kunt ook genoegen nemen met die 40 respondenten die je hebt, dan heb je een foutmarge van 12 procent.
Kijk maar eens goed rond op de site http://www.allesovermarktonderzoek.nl/Extra/Steekproef.aspx
Mvg
Thijs Bouten

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 7 mei 2011
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








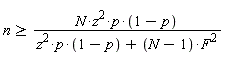
 tevreden, ja of nee... Om safe te spelen stel je dat de beide uitkomsten even veel kans hebben.
tevreden, ja of nee... Om safe te spelen stel je dat de beide uitkomsten even veel kans hebben.