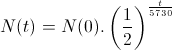|
|
|
\require{AMSmath}



Exponentiele formule
Hieronder een vraag waar ik niet echt uit kom. Vraag a en b gingen wel, maar c is me toch wel lastig. Iemand die mij kan helpen?
Elk levend organisme bevat een hoeveelheid radioactieve koolstof C14. Per kilogram organisch materiaal is dat ongeveer een miljoenste milligram. Zodra het organisme sterft, vindt er geen uitwisseling meer plaats met de koolstof uit de atmosfeer. De hoeveelheid C14 in het dode organisme neemt vanaf dat moment exponentieel af. Na elke periode van 5730 jaar is de hoeveelheid C14 gehalveerd. De ouderdom van allerlei archeologische vondsten kan dus geschat woren aan de hand van de nog aanwezige hoeveelheid C14.
C) Bij opgravingen wordt een skelet van een mammoet gevonden. Het skelet weegt 7500 kg. Na onderzoek wordt vastgesteld dat er nog 0,0022 mg C14 aanwezig is in het skelet. Hoeveel jaar geleden is deze mammoet volgens de C14 methode gestorven?
Vriendelijk bedankt
Laila
Leerling bovenbouw havo-vwo - maandag 24 januari 2011
Antwoord
Hallo
Je kent de formule :
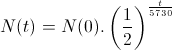
waarbij N(0) de beginconcentratie (is gegeven)
en N(t) de concentratie na t jaren (is eveneens gegeven).
Je bekomt dus een vergelijking van de aard :
A = B.(1/2)x
Hieruit kun je x berekenen met behulp van een logaritme.
Lukt het zo?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 24 januari 2011
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|