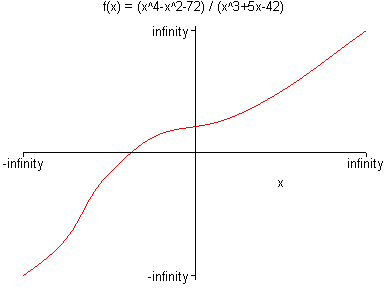WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Limieten met 0/0

hallo! ik snap niet helemaal hoe je dit moet oplossen , als jullie deze kunnun uitwerken kom ik al veel verder.

lim (x⁴-x²-72)/(x³+5x-42)
x-3

lim met x-[oo] snap ik wel maar hoe deze moet weet ik niet. en wat reken je nu eiglijk uit?? alvast bedankt!
Anna v
Leerling bovenbouw havo-vwo - maandag 6 januari 2003

Antwoord

Beste Anna,

Meestal helpt herschrijven van de functie waarvan je de limiet neemt wel, maar in dit geval blijf je uitkomen op de onbepaaldheid 0/0. Nu is hier een truckje voor.
Indien je een onbepaaldheid uitkomt bij limieten, dan mag je de regel van L'Hopital toepassen (onbepaald wil dus zeggen 0/0, ¥/¥, ...).
Hoe die regel algemeen werkt kun je in de database opzoeken, maar hier toegepast wordt die regel : differentieer de teller en deel door de afgeleide van de noemer. Dan vul je de limiet in en indien er dan nog een onbepaaldheid uitkomt herhaal je de procedure totdat een waarde uitkomt.

Hier dus
(x⁴ - x² - 72)'
---------------
(x³ + 5x - 42)'
4x³ - 2x
---------
3x² + 5

Dus de limiet voor x gaande naar 3 is 3 3/16, dus y streeft naar de waarde 3 3/16. Wat betekent dit? Aangezien de functie onbepaald is indien we rechtstreeks x = 3 invoeren, moet je 'n methode toepassen waardoor je de onbepaaldheid omzeilt.

Een andere methode dan de regel van L'Hopital toe te passen was x = 3 zo goed mogelijk te benaderen, door eerst de waarden x = 2,9 daarna x = 2,99 ; x = 2,999 etc.
En ook x = 3,1; x = 3,01 ; x = 3,001 etc.
Dan bepaal je welke waarde er ongeveer uitkomt.
Je zult merken dat f(3,000001) f(2.999999) namelijk 3,1875 (hetgeen overeenkomt met L'Hopital).

Voor de limiet gaande naar +¥ moet je 3 keer de regel van L'Hopital toepassen en krijg je als waarde + ¥.
Voor -¥ dezelfde methode als +¥ alleen is de y-waarde -¥.
Je kunt natuurlijk ook steeds groter wordende getallen van x invullen en zo +oneindig benaderen, en steeds kleinere getallen invullen om -oneindig te benaderen.
De grafiek getekend van -oneindig tot +oneindig van de functie (x^4-x^2-72)/(x^3+5*x-42) kun je hieronder vinden.

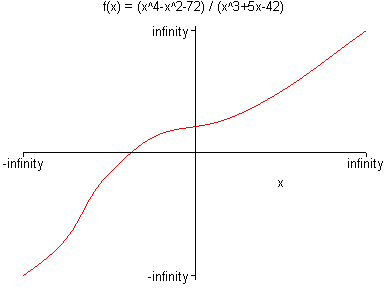
Zie vraag 4419

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 6 januari 2003