WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hexagram

In de magische ster (hexagram) met cijfers 1 t/m 12 probeer ik een algoritme te bedenken voor het volgende:

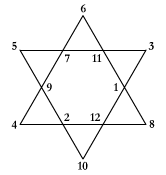
Bij dit voorbeeld is de som elke rechte lijn met vier getallen gelijk aan 26.

Maar ik wil ook er voor zorgen dat de zes hoekpunten een totaal van 26 opleveren. Ik heb het een en het ander op internet gezocht maar heb niet echt kunnen achterhalen hoe ik hier een algoritme kan maken om de som van elke rechtelijn met vier getallen aan 26 gelijk te stellen en dat de 6 hoekpunten ook gelijk zijn aan 26.
Ik hoop dat u mij hiermee kunt helpen of iig goed de weg kan wijzen.

Groeten.
Gerard
Student universiteit - maandag 13 december 2010

Antwoord

Hallo, Gerard.

Je moet de twaalf punten van ster en zeshoek nummeren, bijvoorbeeld in volgorde van opklimmende afstand tot de onderkant van het scherm, en, bij gelijke afstand tot de onderkant van het scherm, in volgorde van opklimmende afstand tot de linkerkant van het scherm.

Dan moet je verder het gepaste stelsel lineaire vergelijkingen opstellen, en dit stelsel oplossen.

Bedoel je de zes hoekpunten van de ster?
Het gepaste stelsel is dan:
x₂+x₃+x₄+x₅ = 26
x₈+x₉+x₁₀+x₁₁ = 26
x₁+x₃+x₆+x₈ = 26
x₁+x₄+x₇+x₁₁ = 26
x₂+x₆+x₉+x₁₂ = 26
x₅+x₇+x₁₀+x₁₂ = 26
x₁+x₅+x₁₁+x₁₂+x₈+x₂ = 26.

(Als je de zes hoekpunten van de binnenste zeshoek bedoelt, moet je de laatste vergelijking vervangen door
x₃+x₄+x₇+x₁₀+x₉+x₆ = 26.)

Schrijf nu het stelsel in de matrixvorm en los het op met de standaardtechniek van het 'vegen'.
Op deze manier vind je in parametervorm ALLE oplossingen.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 15 december 2010

Re: Hexagram