|
|
|
\require{AMSmath}



Formules voor piramidegetallen in de driehoek van Pascal
Piramideformules. Geef ook 2 formules voor P(n). De eerste drukt P(n) uit in D(n), D(n-1) en wat je verder nog meer nodig hebt (kortom, een piramidegetal wordt uitgedrukt in uitsluitend driehoeksgetallen). De tweede drukt P(n) uit in P(n-1) en D(n).
Remco
Leerling bovenbouw havo-vwo - woensdag 10 december 2003
Antwoord

Ik neem aan dat je het hebt over de piramidegetallen zoals je die ook tegen komt op Bijzondere getallen in de driehoek van Pascal.
Er zijn een heleboel verschillende piramidegetallen, net als bij een 'gewone' piramide kan je verschillende vormen tegen komen, met een driehoekige stapeling, een vierkante stapeling, een vijfhoekige enz. Op Polyhedral Numbers kan je er meer over vinden.
Nu de vierkante piramide getallen. In de driehoek van Pascal kan je ze (zoals gezegd) ook vinden:
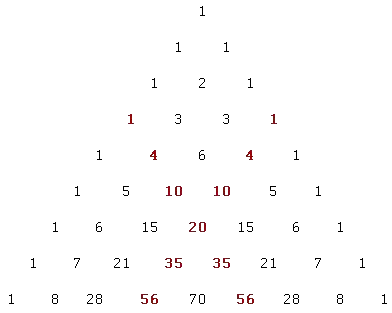
Dus: 1, 4, 10, 20, 35, 56,...
Precies schuin daarboven zitten de driehoeksgetallen en als je goed kijkt dan zie je dat tussen zo'n piramidegetal en de driehoeksgetallen erboven een verband bestaat! (Ook wel de sok van de driehoek van Pascal genoemd)
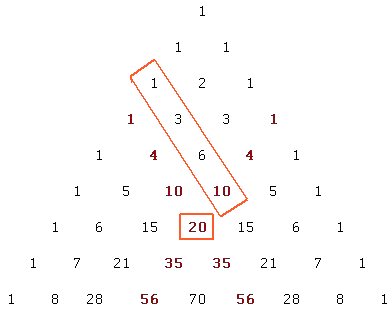
..en alsof dat nog niet genoeg is bestaat het vierde piramidegetal dus uit 4 driehoeksgetallen... nou ja, dan vraag ik je! Zou dat altijd zo zijn? Kan je dan niet heel makkelijk een 'uitdrukking' bedenken voor P(n)? Zou dat altijd zo zijn? Kan je dan niet heel makkelijk een 'uitdrukking' bedenken voor P(n)?
Die andere 'uitdrukking' is nu ook niet zo moeilijk meer..., want als je P(n) kunt uitdrukken in driehoeksgetallen kan je dat met P(n-1) ook.. en dan... weet je 't dan? Trouwens in de driehoek van Pascal kan je de formule eigenlijk al zo zien! Open de ogen!
Zou 't lukken? Vast wel...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 10 december 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











 Zou dat altijd zo zijn? Kan je dan niet heel makkelijk een 'uitdrukking' bedenken voor P(n)?
Zou dat altijd zo zijn? Kan je dan niet heel makkelijk een 'uitdrukking' bedenken voor P(n)?
